题目内容
14.已知数列{an},a1=1,${a_{n+1}}=\frac{{2{a_n}}}{{{a_n}+2}}$,则a10的值为( )| A. | 5 | B. | $\frac{1}{5}$ | C. | $\frac{11}{2}$ | D. | $\frac{2}{11}$ |
分析 利用数列的递推公式推导出数列{an}的前四项,从而猜想an=$\frac{2}{n+1}$.并利用利用数学归纳法进行证明得到${a}_{n}=\frac{2}{n+1}$,由此能求出a10.
解答 解:∵数列{an},a1=1,${a_{n+1}}=\frac{{2{a_n}}}{{{a_n}+2}}$,
∴${a}_{2}=\frac{2×1}{1+3}$=$\frac{2}{3}$,
${a}_{3}=\frac{2×\frac{2}{3}}{\frac{2}{3}+2}$=$\frac{2}{4}$,
${a}_{4}=\frac{2×\frac{1}{2}}{\frac{1}{2}+2}$=$\frac{2}{5}$,
由此猜想an=$\frac{2}{n+1}$.
下面利用数学归纳法进行证明:
①${a}_{1}=\frac{2}{1+1}=1$,成立;
②假设ak=$\frac{2}{k+1}$,
则${a}_{k+1}=\frac{2{a}_{k}}{{a}_{k}+2}$=$\frac{\frac{4}{k+1}}{\frac{2}{k+1}+2}$=$\frac{2}{(k+1)+1}$,成立,
∴${a}_{n}=\frac{2}{n+1}$,
∴a10=$\frac{2}{11}$.
故选:D.
点评 本题考查数列的第10项的求法,是中档题,解题时要认真审题,注意递推公式、数学归纳法的合理运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
7.函数f(x)=3x+2x-3的零点所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
3.某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )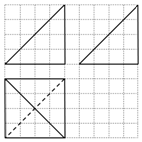

| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
10.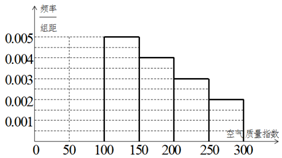 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
该社团将该校区在2016年连续100天的空气质量指数数据作为样本,绘制了如图的频率分布表,将频率视为概率.估算得全年空气质量等级为2级良的天数为73天(全年以365天计算).
(Ⅰ)求x,y,a,b的值;
(Ⅱ)请在答题卡上将频率分布直方图补全(并用铅笔涂黑矩形区域),并估算这100天空气质量指数监测数据的平均数.
 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
(Ⅱ)请在答题卡上将频率分布直方图补全(并用铅笔涂黑矩形区域),并估算这100天空气质量指数监测数据的平均数.
19.执行如图所示的程序框图,输出S的值为( )
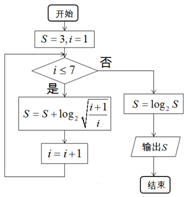

| A. | log210-1 | B. | 2log23-1 | C. | $\frac{9}{2}$ | D. | 6 |
3.从某高校在校大学生中随机选取5名女大学生,由她们身高和体重的数据得到的回归直线方程为$\widehat{y}$=0.79x-73.56,数据列表是:
则其中的数据a=163.
| 身高x(cm) | 155 | 161 | a | 167 | 174 |
| 体重y(kg) | 49 | 53 | 56 | 58 | 64 |
2.已知点A(0,2),动点P(x,y)满足条件$\left\{\begin{array}{l}{x≥0}\\{y≤2x}\\{3x-y≤6}\end{array}\right.$则|PA|的最小值是( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |