题目内容
1.定义在R上的偶函数f(x)满足f(2-x)=f(x),且当x∈[1,2]时,f(x)=lnx-x+1,若函数g(x)=f(x)+mx有7个零点,则实数m的取值范围为( )| A. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | B. | $(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | ||
| C. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})$ | D. | $(\frac{1-ln2}{8},\frac{ln2-1}{6})$ |
分析 确定函数为偶函数则其周期为T=2,函数在x∈[1,2]为减函数,作出函数的图象,得出当x<0时,要使符合题意则$m∈(\frac{ln2-1}{6},\frac{ln2-1}{8})$,根据偶函数的对称性,当x>0时,要使符合题意则$m∈(\frac{1-ln2}{8},\frac{1-ln2}{6})$.即可得出结论.
解答 解:因为函数f(2-x)=f(x)可得图象关于直线x=1对称,且函数为偶函数则其周期为T=2,
又因为$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$,当x∈[1,2]时有f'(x)≤0,则函数在x∈[1,2]为减函数,
作出其函数图象如图所示:
其中${k_{OA}}=\frac{ln2-1}{6},{k_{OB}}=\frac{ln2-1}{8}$,当x<0时,要使符合题意则$m∈(\frac{ln2-1}{6},\frac{ln2-1}{8})$
根据偶函数的对称性,当x>0时,要使符合题意则$m∈(\frac{1-ln2}{8},\frac{1-ln2}{6})$.
综上所述,实数m的取值范围为$(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$,
故选A.
点评 本题考查函数的奇偶性、单调性,考查数形结合的数学思想,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.抛物线$y=\frac{1}{4}{x^2}$的焦点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
10.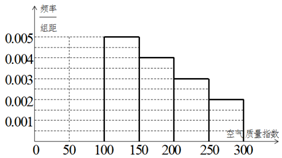 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
该社团将该校区在2016年连续100天的空气质量指数数据作为样本,绘制了如图的频率分布表,将频率视为概率.估算得全年空气质量等级为2级良的天数为73天(全年以365天计算).
(Ⅰ)求x,y,a,b的值;
(Ⅱ)请在答题卡上将频率分布直方图补全(并用铅笔涂黑矩形区域),并估算这100天空气质量指数监测数据的平均数.
 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
(Ⅱ)请在答题卡上将频率分布直方图补全(并用铅笔涂黑矩形区域),并估算这100天空气质量指数监测数据的平均数.
16.已知全集U=R,集合A={x|y=lgx},集合B=$\left\{{y|y=\sqrt{x}+1}\right\}$,那么A∩(∁UB)=( )
| A. | ∅ | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |
10.下列结论中错误的是( )
| A. | 若0<α<$\frac{π}{2}$,则sinα<tanα | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4}{5}$ | |
| D. | 若扇形的周长为6,半径为2,则其中心角的大小为1弧度 |
9.一个几何体的三视图如图所示(单位:cm),则此几何体的表面积是( )
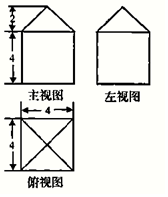

| A. | 96+16$\sqrt{2}$cm2 | B. | 80+16$\sqrt{2}$cm2 | C. | 96+32$\sqrt{2}$cm2 | D. | 80+32$\sqrt{2}$cm2 |