题目内容
18．下列函数中，既是偶函数，又在区间（1，2）上是减函数的为（ ）| A． | y=log${\;}_{\frac{1}{2}}$|x| | B． | y=x${\;}^{\frac{1}{2}}$ | C． | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D． | y=lg$\frac{2-x}{2+x}$ |
分析 根据函数单调性和奇偶性的性质分别进行判断即可．
解答 解：对于A，既是偶函数，又在区间（1，2）上是减函数；
对于B，函数的定义域不关于原点对称，不表示偶函数；
对于C，是偶函数，在区间（1，2）上是增函数；
对于D，是奇函数．
故选A．
点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
相关题目
10．一袋中装有大小相同，编号分别为1，2，3，4，5，6，7，8的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号之和不小于15的概率为（ ）
| A． | $\frac{1}{32}$ | B． | $\frac{1}{64}$ | C． | $\frac{3}{64}$ | D． | $\frac{3}{32}$ |
10．
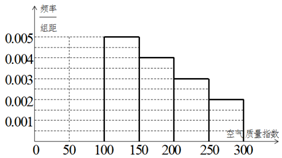某中学环保社团参照国家环境标准，制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过300）：
该社团将该校区在2016年连续100天的空气质量指数数据作为样本，绘制了如图的频率分布表，将频率视为概率．估算得全年空气质量等级为2级良的天数为73天（全年以365天计算）．
（Ⅰ）求x，y，a，b的值；
（Ⅱ）请在答题卡上将频率分布直方图补全（并用铅笔涂黑矩形区域），并估算这100天空气质量指数监测数据的平均数．
某中学环保社团参照国家环境标准，制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过300）：| 空气质量指数 | （0，50] | （50，100] | （100，150] | （150，200] | （200，250] | （250，300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| （0，50] | x | a |
| （50，100] | y | b |
| （100，150] | 25 | 0.25 |
| （150，200] | 20 | 0.2 |
| （200，250] | 15 | 0.15 |
| （250，300] | 10 | 0.1 |
（Ⅱ）请在答题卡上将频率分布直方图补全（并用铅笔涂黑矩形区域），并估算这100天空气质量指数监测数据的平均数．
3．从某高校在校大学生中随机选取5名女大学生，由她们身高和体重的数据得到的回归直线方程为$\widehat{y}$=0.79x-73.56，数据列表是：
则其中的数据a=163．
| 身高x（cm） | 155 | 161 | a | 167 | 174 |
| 体重y（kg） | 49 | 53 | 56 | 58 | 64 |
10．下列结论中错误的是（ ）
| A． | 若0＜α＜$\frac{π}{2}$，则sinα＜tanα | |
| B． | 若α是第二象限角，则$\frac{α}{2}$为第一象限或第三象限角 | |
| C． | 若角α的终边过点P（3k，4k）（k≠0），则sinα=$\frac{4}{5}$ | |
| D． | 若扇形的周长为6，半径为2，则其中心角的大小为1弧度 |
7．已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的一个交点，点B是点F关于坐标原点的对称点，且以AB为直径的圆过点F，则双曲线的离心率为（ ）
| A． | 2$\sqrt{2}$-1 | B． | $\sqrt{2}$+1 | C． | 8$\sqrt{2}$-8 | D． | 2$\sqrt{2}$-2 |
过点
，则
______，准线方程是______.