题目内容
在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=
b,2sinC+2sin(A-B)+
cos2A=
(1)求角B的大小.
(2)若a=2,a<c求△ABC的面积S.
| 2 |
| 6 |
| 6 |
(1)求角B的大小.
(2)若a=2,a<c求△ABC的面积S.
考点:正弦定理
专题:计算题,解三角形
分析:(1)利用两角和与差的三角函数公式、二倍角公式,化简题中的三角函数等式得2cosB=
sinA,然后利用a=
b算出sinA=
sinB,从而得出tanB的值,可得角B的大小.
(2)首先算出边b=
a=
,再根据(1)的结论及a<c算出角A=
,进而算出sinC的值,最后利用三角形的面积公式加以计算,可得△ABC的面积S.
| 6 |
| 2 |
| 2 |
(2)首先算出边b=
| ||
| 2 |
| 2 |
| π |
| 4 |
解答:
解:(1)∵2sinC+2sin(A-B)+
cos2A=
,
∴2sin(A+B)+2sin(A-B)=
(1-cos2A),
即2sinAcosB=
sin2A,
结合sinA>0,化简得2cosB=
sinA.
∵a=
b,∴由正弦定理可得sinA=
sinB.
因此,可得tanB=
=
,
而在△ABC中B∈(0,π),所以角B=
;
(2)∵a=
b,∴由正弦定理可得sinA=
sinB.
∴sinA=
sin
=
,
根据a<c得到A<C.
∴A=
,b=
,sinC=sin(A+B)=sin
=
,
△ABC的面积S=
absin
=
×2×
×
=
.
| 6 |
| 6 |
∴2sin(A+B)+2sin(A-B)=
| 6 |
即2sinAcosB=
| 6 |
结合sinA>0,化简得2cosB=
| 6 |
∵a=
| 2 |
| 2 |
因此,可得tanB=
| sinB |
| cosB |
| ||
| 3 |
而在△ABC中B∈(0,π),所以角B=
| π |
| 6 |
(2)∵a=
| 2 |
| 2 |
∴sinA=
| 2 |
| π |
| 6 |
| ||
| 2 |
根据a<c得到A<C.
∴A=
| π |
| 4 |
| 2 |
| 5π |
| 12 |
| ||||
| 4 |
△ABC的面积S=
| 1 |
| 2 |
| 5π |
| 12 |
| 1 |
| 2 |
| 2 |
| ||||
| 4 |
| ||
| 2 |
点评:本题给出三角形ABC满足的条件,求角B的大小,并求三角形的面积.着重考查了三角恒等变换公式、正余弦定理与三角形的面积公式等知识,属于中档题.

练习册系列答案
相关题目
将圆x2+y2=1向右平移2个单位,向下平移1个单位后,恰好与直线x-y+b=0相切,则实数b的值为( )
A、3±
| ||
B、-3±
| ||
C、2±
| ||
D、-2±
|
与57°角的终边相同的角的集合是( )
| A、{α|α=57°+k•360°,k∈Z} |
| B、{α|α=-157°+k•360°,k∈Z} |
| C、{α|α=33°+k•360°,k∈Z} |
| D、{α|α=-33°+k•360°,k∈Z} |
设集合A={x|
<x<2},B={x|x2<1},则A∪B=( )
| 1 |
| 2 |
| A、{x|1<x<2} | ||
| B、{x|-1<x<2} | ||
C、{x|
| ||
| D、{x|-1<x<1} |
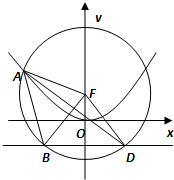 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4 某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.