题目内容
若y=f(x)在定义域上为增函数,试判断y=-f(x),y=f(-x)f(
)的单调性.
| 1 |
| x |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:由y=f(x)在定义域上为增函数,得出y=-f(x)、y=f(-x)、y=f(
)的增减性;从而得出y=f(-x)f(
)的增减性.
| 1 |
| x |
| 1 |
| x |
解答:
解:∵y=f(x)在定义域上为增函数,
∴f′(x)≥0,
∴(-f(x))′=-f′(x)≤0,
∴函数y=-f(x)是定义域上的减函数;
同理,函数f(-x)是定义域上的减函数,
函数f(
)也是定义域上的减函数;
∴函数y=f(-x)f(
)是定义域上的增函数.
∴f′(x)≥0,
∴(-f(x))′=-f′(x)≤0,
∴函数y=-f(x)是定义域上的减函数;
同理,函数f(-x)是定义域上的减函数,
函数f(
| 1 |
| x |
∴函数y=f(-x)f(
| 1 |
| x |
点评:本题考查了复合函数的单调性问题,解题时应明确复合函数的单调性问题,是基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
如果执行如图的程序框图,那么输出的S等于( )


| A、45 | B、55 | C、90 | D、110 |
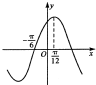 如图所示是函数f(x)=sin(?x+φ)(?>0,|φ|<π)的部分图象,则f(x)的解析式为
如图所示是函数f(x)=sin(?x+φ)(?>0,|φ|<π)的部分图象,则f(x)的解析式为