题目内容

记实数x1，x2，…xn中的最小数为min{x1，x2，…xn}，设函数f（x）=min{1+sinωx，1-sinωx}（ω＞0），若f（x）的最小正周期为1，则ω的值为（　　）
A、
1
2
B、1
C、
π
2
D、π
考点：函数的最值及其几何意义
专题：三角函数的图像与性质
分析：结合函数y=1+sinωx和y=1-sinωx的图象关系，确定函数f（x）与y=1+sinωx和y=1-sinωx的周期关系即可得到结论．
解答： 解：y=1+sinωx和y=1-sinωx的图象关于y=1对称，
则函数f（x）的周期为y=1+sinωx的周期的一半，
若f（x）的最小正周期为1，则y=1+sinωx的周期为2，
即T=
2π
ω
=2，解得ω=π，
故选：D
点评：本题主要考查三角函数周期的计算，根据条件确定函数f（x）的周期关系与y=1+sinωx的周期关系是解决本题的关键．
练习册系列答案
相关题目
已知向量
a
=（x，y），
b
=（1，-2），从六张大小相同、分别标有号码1、2、3、4、5、6的卡片中，有放回地抽取两张x，y分别表示第一次，第二次抽取的卡片上的号码，求满足
a
•
b
=-1的概率．
设数列{an}的前n项和为Sn，已知2an-2n=Sn，则数列{an}的通项公式an=
 
．
已知命题p：x2-2x-3＞0，命题q：
1
3-x
＞1，若￢q且p为真．则x的取值范围
 
．
写出命题“x＞1”的一个必要条件是
 
．
已知函数y=f（x+1）的图象关于点（-1，0）对称，且当x∈（-∞，0）时．f（x）+xf′（x）＜0成立（其中f（x）是f（x）的导函数），若a=(
3
0.3
 
)•f(
3
0.3
 
)，b=(logπ3)•f(logπ3)，c=(log3
1
9
)•f(log3
1
9
)，则a，b，c从大到小的次序为
 
．
已知函数f（x）=x2-2x+a有且仅有一个零点．
（1）求实数a的值；
（2）当x∈[1，4]时，求f（x）的取值范围．
如图是某一个几何体的三视图，则该几何体的体积为
 
．
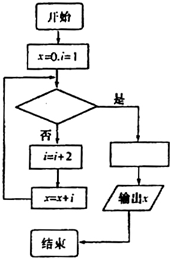如图是某同学求50个奇数3，5，7，…，101的平均数而设计的程序框图的部分内容，则在该程序框图中的空白判断框和处理框中应填入的内容依次是（　　）
A、i＞100，x=
x
50
B、i≥100，x=
x
100
C、i＜100，x=
x
50
D、i≤100，x=
x
100

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网