题目内容
| 2cos25°-cos85° | ||
sin25°+
|
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由两角和与差的正弦函数公式展开后根据诱导公式化简即可求值．
解答：
解：
=
=
=
=
．
故答案为：
．
| 2cos25°-cos85° | ||
sin25°+
|
| 2sin65°-sin5° |
| 2sin(25°+60°) |
| 2sin60°cos5°+2cos60°sin5°-sin5° |
| 2cos5° |
| ||
| 2cos5° |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题主要考查了两角和与差的正弦函数公式，诱导公式化简求值，属于基本知识的考查．
练习册系列答案
快乐5加2金卷系列答案
相关题目
已知f（x）为奇函数，且在（-∞，0）内是增函数，又f（-2）=0，则f（x）＜0的解集为（ ）
| A、（-2，0）∪（0，2） |
| B、（-∞，-2）∪（0，2） |
| C、（-∞，-2）∪（2，+∞） |
| D、（-2，0）∪（2，+∞） |
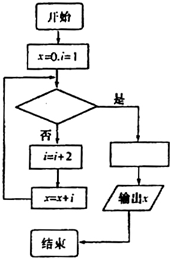如图是某同学求50个奇数3，5，7，…，101的平均数而设计的程序框图的部分内容，则在该程序框图中的空白判断框和处理框中应填入的内容依次是（ ）A、i＞100，x=
| ||
B、i≥100，x=
| ||
C、i＜100，x=
| ||
D、i≤100，x=
|
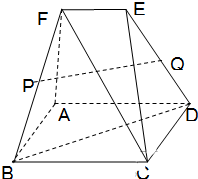如图，多面体ABCDEF中，四边形ABCD是边长为2a的正方形，平面ADEF垂直于平面ABCD，且FA⊥AD，EF∥AD，EF=AF=a．