题目内容
如图,在四棱锥E﹣ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(1)求证:DE∥平面FGH;
(2)若点P在直线GF上,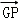 =λ
=λ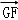 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为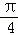 ,求λ的值.
,求λ的值.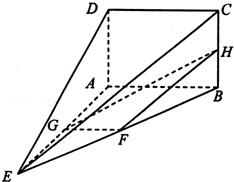
(1)证明见解析;(2)λ的值等于1或4.
解析试题分析:(1)取AD的中点M,连接MH,MG,由G、H、F分别是AE、BC、BE的中点,得MH∥GF,G、F、H、M四点共面,又MG∥DE,所以DE∥平面MGFH;(2)在平面ABE内过A作AB的垂线,记为AP,则AP⊥平面ABCD.以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴,建立建立空间直角坐标系A﹣xyz,如图所示.可得 坐标,利用空间向量的坐标运算求出平面PBD的一个法向量=(5﹣2λ,
坐标,利用空间向量的坐标运算求出平面PBD的一个法向量=(5﹣2λ, ,2
,2 )
) ,再由图可知平面ABP的一个法向量为
,再由图可知平面ABP的一个法向量为 ,由cos<
,由cos< >=
>= =
= 得λ=1或4.
得λ=1或4.
解:(1)证明:取AD的中点M,连接MH,MG.
∵G、H、F分别是AE、BC、BE的中点,
∴MH∥AB,GF∥AB,
∴MH∥GF,即G、F、H、M四点共面,平面FGH即平面MGFH,
又∵△ADE中,MG是中位线,∴MG∥DE
∵DE?平面MGFH,MG?平面MGFH,
∴DE∥平面MGFH,即直线DE与平面FGH平行.
(2)在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.
以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴,
建立建立空间直角坐标系A﹣xyz,如图所示.
可得A(0,0,0),B(0,4,0),D(0,0,2),E(2 ,﹣2,0),G(
,﹣2,0),G( ,﹣1,0),F(
,﹣1,0),F( ,1,0)
,1,0)
∴ =(0,2,0),
=(0,2,0), =(0,﹣4,2),
=(0,﹣4,2), =(
=( ,﹣5,0).
,﹣5,0).
由 =λ
=λ =(0,2λ,0),可得
=(0,2λ,0),可得 =
= +
+ =(
=( ,2λ﹣5,0).
,2λ﹣5,0).
设平面PBD的法向量为 =(x,y,z),
=(x,y,z),
则 ,取y=
,取y= ,得z=2
,得z=2 ,x=5﹣2λ,
,x=5﹣2λ,
∴ =(5﹣2λ,
=(5﹣2λ, ,2
,2 ),
),
又∵平面ABP的一个法向量为 =(0,0,1),
=(0,0,1),
∴cos< >=
>= =
= =cos
=cos =
= ,解之得λ=1或4
,解之得λ=1或4
即λ的值等于1或4.
考点:1.线面平行的性质与判定;2.二面角;3.空间想象能力.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案 、
、 为分别取自直线a、b上的单位向量,且
为分别取自直线a、b上的单位向量,且
 ,
,  ,则k=
,则k=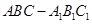 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
,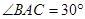 ,
,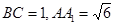 ,点
,点 分别为
分别为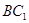 、
、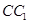 、
、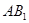 的中点.
的中点.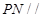 平面
平面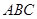 ;
;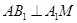 ;
; 的余弦值.
的余弦值.
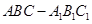 中,点
中,点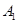 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,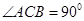 ,
,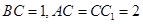 .
.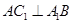 ;
;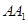 与平面
与平面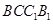 的距离为
的距离为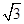 ,求二面角
,求二面角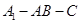 的大小.
的大小.
 中,底面是以
中,底面是以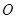 为中心的菱形,
为中心的菱形, 底面
底面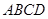 ,
,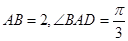 ,
, 为
为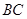 上一点,且
上一点,且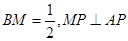 .
.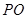 的长;
的长;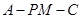 的正弦值.
的正弦值.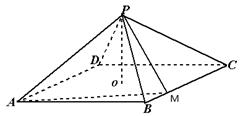
 a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点. .
.
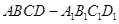 底面
底面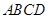 直角梯形,
直角梯形, ∥
∥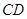 ,
,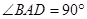 ,
, 是棱
是棱 ,
,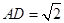 ,
, ,
,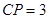 ,
,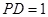 .
.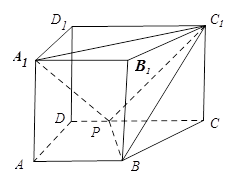
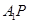 与
与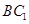 所成的角;
所成的角;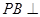 平面
平面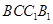 .
.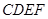 为正方形,面
为正方形,面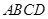 为等腰梯形,
为等腰梯形,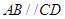 ,
,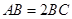 ,
, ,且平面
,且平面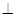 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值;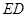 上是否存在点
上是否存在点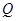 ,使平面
,使平面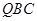 ?
?
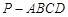 ,底面
,底面 是等腰梯形,
是等腰梯形,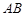 ∥
∥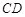 ,
, 是
是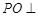 平面
平面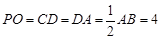 ,
,  是
是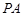 中点.
中点.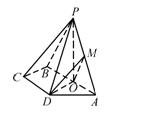
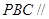 平面
平面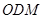 ;
;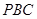 与平面
与平面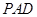 所成锐二面角的余弦值.
所成锐二面角的余弦值.