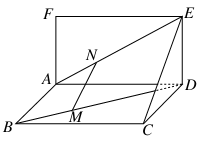
题目内容
如图,三棱柱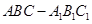 中,点
中,点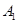 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,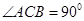 ,
,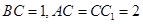 .
.
(1)证明: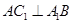 ;
;
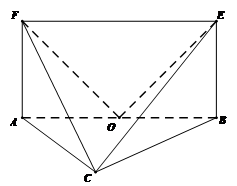
(2)设直线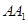 与平面
与平面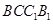 的距离为
的距离为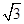 ,求二面角
,求二面角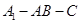 的大小.
的大小.
(1)详见试题分析;(2) (或
(或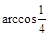 ).
).
解析试题分析:(1)以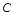 为坐标原点,射线
为坐标原点,射线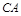 为
为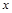 轴的正半轴,以
轴的正半轴,以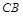 长为单位长,建立空间直角坐标系
长为单位长,建立空间直角坐标系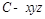 ,计算向量数量积
,计算向量数量积 为0,从而证得
为0,从而证得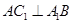 .也可以利用综合法:先由已知
.也可以利用综合法:先由已知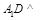 平面
平面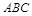 得平面
得平面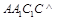 平面
平面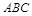 ,再由面面垂直的性质定理证得
,再由面面垂直的性质定理证得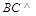 平面
平面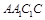 ,而
,而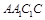 为菱形中
为菱形中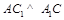 最后由三垂线定理得
最后由三垂线定理得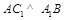 ;(2)向量法:先求平面
;(2)向量法:先求平面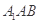 和平面
和平面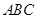 的法向量
的法向量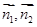 ,再利用公式
,再利用公式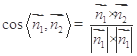 来求二面角
来求二面角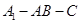 的大小.综合法:先利用三垂线定理或其逆定理作出二面角
的大小.综合法:先利用三垂线定理或其逆定理作出二面角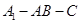 的平面角,再利用解三角形的有关知识求其余弦值大小.
的平面角,再利用解三角形的有关知识求其余弦值大小.
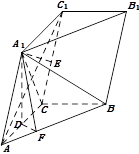
试题解析:解法一:(1)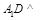 平面
平面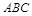 ,
,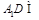 平面
平面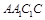 ,故平面
,故平面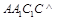 平面
平面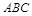 .又
.又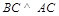 ,
, 平面
平面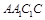 .连结
.连结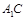 ,∵侧面
,∵侧面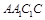 为菱形,故
为菱形,故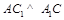 ,由三垂线定理得
,由三垂线定理得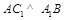 ;(2)
;(2)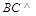 平面
平面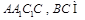 平面
平面 ,故平面
,故平面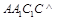 平面
平面 .作
.作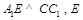 为垂足,则
为垂足,则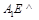 平面
平面 .又直线
.又直线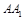 ∥平面
∥平面 ,因而
,因而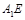 为直线
为直线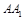 与平面
与平面 的距离,
的距离,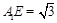 .∵
.∵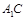 为
为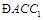 的角平分线,故
的角平分线,故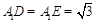 .作
.作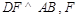 为垂足,连结
为垂足,连结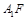 ,由三垂线定理得
,由三垂线定理得 ,故
,故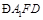 为二面角
为二面角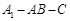 的平面角.由
的平面角.由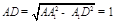 得
得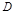 为
为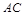 的中点,
的中点,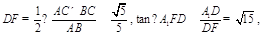 ∴二面角
∴二面角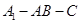 的大小为
的大小为 .
.
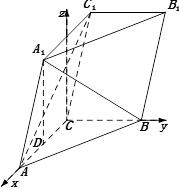
解法二:以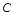 为坐标原点,射线
为坐标原点,射线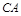 为
为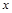 轴的正半轴,以
轴的正半轴,以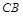 长为单位长,建立如图所示的空间直角坐标系
长为单位长,建立如图所示的空间直角坐标系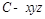 .由题设知
.由题设知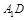 与
与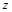

练习册系列答案
相关题目
 ,若
,若 ,则
,则 ______。
______。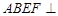 平面
平面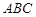 ,四边形
,四边形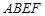 为矩形,
为矩形,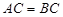 .
.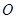 为
为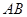 的中点,
的中点,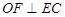 .
.
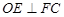 ;
;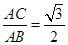 时,求二面角
时,求二面角 的余弦值.
的余弦值.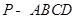 中,
中,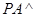 底面
底面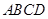 ,
,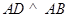 ,
,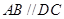 ,
,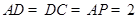 ,
,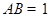 ,点
,点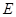 为棱
为棱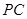 的中点.
的中点. 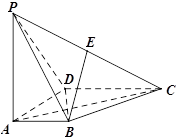
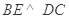 ;
; 与平面
与平面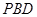 所成角的正弦值;
所成角的正弦值;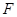 为棱
为棱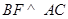 ,求二面角
,求二面角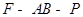 的余弦值.
的余弦值.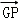 =λ
=λ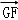 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为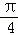 ,求λ的值.
,求λ的值.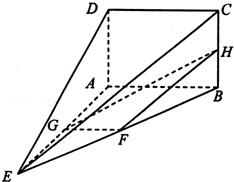

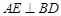 于
于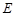 ,延长AE交BC于F,将
,延长AE交BC于F,将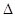 ABD沿BD折起,使平面ABD
ABD沿BD折起,使平面ABD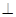 平面BCD,如图2所示.
平面BCD,如图2所示.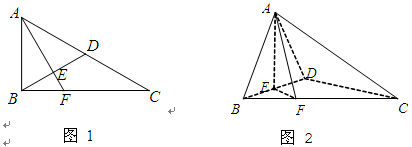
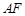 上是否存在点
上是否存在点 使得
使得 平面
平面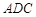 ?若存在,请指明点
?若存在,请指明点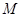 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.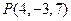 关于平面
关于平面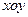 的对称点的坐标为
的对称点的坐标为 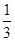 BD,AN=
BD,AN=