题目内容
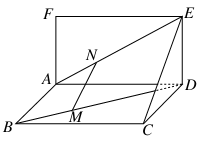
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=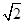 a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
(1)求证:CD⊥面ABB1A1;
(2)在侧棱BB1上确定一点E,使得二面角E-A1C1-A的大小为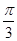 .
.
(1)详见解析;(2)点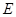 满足
满足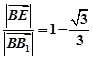 .
.
解析试题分析:(1)由面ACC1A1⊥面ABC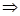 AB⊥面ACC1A1
AB⊥面ACC1A1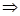 AB⊥CD,由D为AA1中点,AC=A1C可推出CD⊥AA1,从而得到CD⊥面ABB1A1.(2)由题意,以点C为坐标系原点,CA为x轴,过C点平行于AB的直线为y轴,CA1为z轴,建立空间直角坐标系C-xyz,求平面面A1C1A的一个法向量、平面EA1C1的一个法向量,利用向量法
AB⊥CD,由D为AA1中点,AC=A1C可推出CD⊥AA1,从而得到CD⊥面ABB1A1.(2)由题意,以点C为坐标系原点,CA为x轴,过C点平行于AB的直线为y轴,CA1为z轴,建立空间直角坐标系C-xyz,求平面面A1C1A的一个法向量、平面EA1C1的一个法向量,利用向量法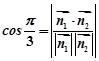 求解.
求解.
(1)【证】∴面ACC1A1⊥面ABC,AB⊥AC
∴AB⊥面ACC1A1,即有AB⊥CD;
又AC=A1C,D为AA1中点,则CD⊥AA1 ∴CD⊥面ABB1A1.(6分)
(2)【解】如图所示以点C为坐标系原点,CA为x轴,过C点平行于AB的直线为y轴,CA1为z轴,建立空间直角坐标系C-xyz,则有A(a,0,0),B(a,a,0),A1(0,0,a), B1(0,a,a)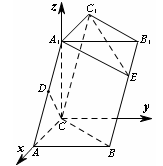
C1(-a,0,a),设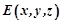 ,且
,且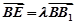 ,
,
即有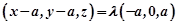
所以E点坐标为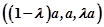
由条件易得面A1C1A的一个法向量为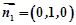
设平面EA1C1的一个法向量为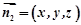 ,
,
由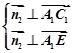 可得
可得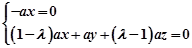
令y=1,则有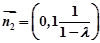 ,(9分)
,(9分)
则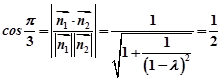 ,得
,得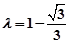 ,
,
∴当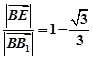 时,二面角E-A1C1-A的大小为
时,二面角E-A1C1-A的大小为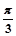 .(12分)
.(12分)
考点:空间中的线线垂直、线面垂直、面面垂直,向量法求解空间角.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
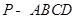 中,
中,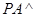 底面
底面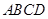 ,
,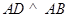 ,
,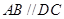 ,
,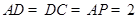 ,
,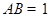 ,点
,点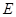 为棱
为棱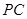 的中点.
的中点. 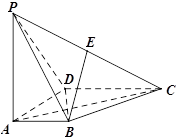
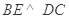 ;
; 与平面
与平面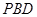 所成角的正弦值;
所成角的正弦值;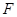 为棱
为棱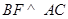 ,求二面角
,求二面角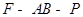 的余弦值.
的余弦值.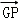 =λ
=λ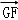 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为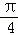 ,求λ的值.
,求λ的值.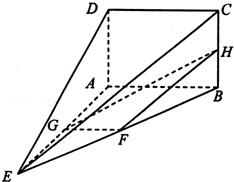


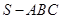 中,
中,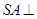 底面
底面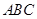 ,点
,点 为以
为以 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且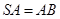 ,点
,点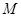 是
是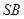 的中点,
的中点,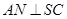 且交
且交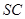 于点
于点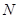 .
. 面
面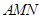 ;
;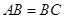 时,求二面角
时,求二面角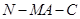 的余弦值.
的余弦值.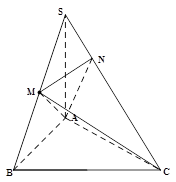
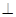 底面ABCD,PD
底面ABCD,PD ,
, ,
,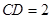 .
.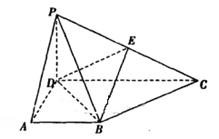
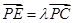 ,试确定
,试确定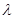 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为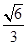 .
. 中,AA1=AB=4,AD=2,
中,AA1=AB=4,AD=2,
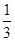 BD,AN=
BD,AN=