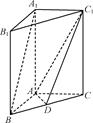
题目内容
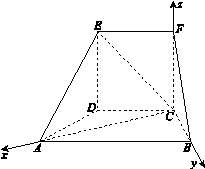
如图所示的几何体中,面 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形, ,
,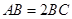 ,
, ,且平面
,且平面
 平面
平面 .
.
(1)求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)线段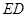 上是否存在点
上是否存在点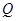 ,使平面
,使平面
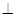 平面
平面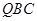 ?
?
证明你的结论.
(1) 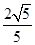 , (2)详见解析.
, (2)详见解析.
解析试题分析:(1)利用空间向量求线面角,关键求出面的一个法向量. 先由面面垂直得到线面垂直,即由平面
 面
面 ,得
,得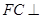 平面
平面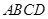 .建立空间直角坐标系,表示各点坐标,得
.建立空间直角坐标系,表示各点坐标,得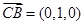 ,设平面
,设平面 的法向量为
的法向量为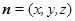 ,则有
,则有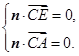 所以
所以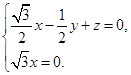 取
取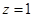 ,得
,得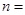
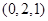 .根据
.根据 与平面
与平面 所成的角正弦值等于
所成的角正弦值等于 与平面
与平面 法向量夹角余弦值的绝对值,得到
法向量夹角余弦值的绝对值,得到 与平面
与平面 所成角的正弦值为
所成角的正弦值为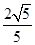 .(2) 假设线段
.(2) 假设线段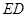 上存在点
上存在点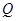 ,设
,设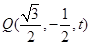
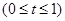 ,可求出平面
,可求出平面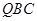 的一个法向量
的一个法向量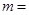
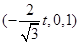 .要使平面
.要使平面
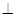 平面
平面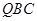 ,只需
,只需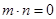 ,即
,即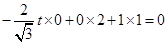 ,此方程无解,所以线段
,此方程无解,所以线段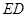 上不存在点
上不存在点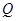 ,使平面
,使平面
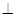 平面
平面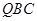 .
.
(1)因为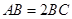 ,
,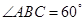 ,
,
在△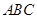 中,由余弦定理可得
中,由余弦定理可得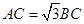 ,
,
所以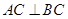 . 又因为
. 又因为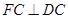
平面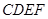
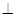 面
面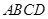 ,所以
,所以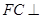 平面
平面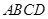 .
.
所以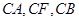 两两互相垂直,
两两互相垂直,
如图建立空间直角坐标系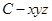 .
.
设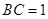 ,所以
,所以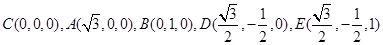 .
.
所以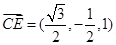 ,
,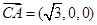 ,
,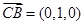 .
.
设平面 的法向量为
的法向量为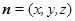 ,则有
,则有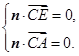
所以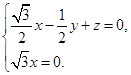 取
取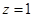 ,得
,得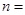
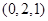 .
.
设 与平面
与平面 所成的角为
所成的角为 ,则
,则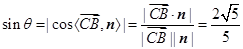 ,
,
所以 与平面
与平面 所成角的正弦值为
所成角的正弦值为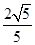 .
.
(2)线段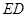 上不存在点
上不存在点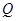 ,使平面
,使平面

练习册系列答案
相关题目
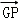 =λ
=λ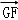 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为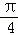 ,求λ的值.
,求λ的值.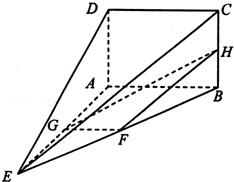

 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.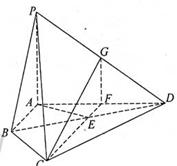
 中,
中,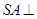 底面
底面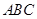 ,点
,点 为以
为以 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且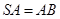 ,点
,点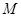 是
是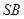 的中点,
的中点,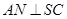 且交
且交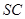 于点
于点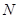 .
. 面
面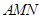 ;
;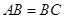 时,求二面角
时,求二面角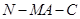 的余弦值.
的余弦值.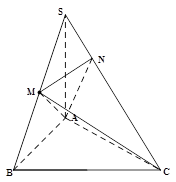
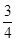 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4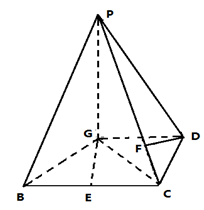
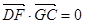 ,
,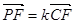 ,求
,求 的值.
的值.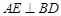 于
于 ,延长AE交BC于F,将
,延长AE交BC于F,将 ABD沿BD折起,使平面ABD
ABD沿BD折起,使平面ABD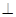 平面BCD,如图2所示.
平面BCD,如图2所示.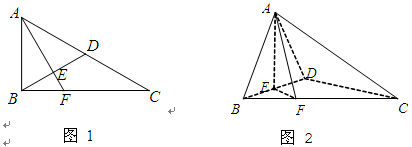
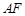 上是否存在点
上是否存在点 使得
使得 平面
平面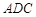 ?若存在,请指明点
?若存在,请指明点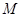 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.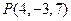 关于平面
关于平面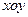 的对称点的坐标为
的对称点的坐标为