题目内容
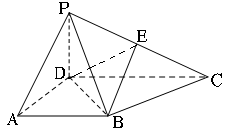
如图,四棱锥 中,底面是以
中,底面是以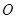 为中心的菱形,
为中心的菱形, 底面
底面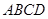 ,
,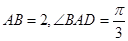 ,
, 为
为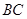 上一点,且
上一点,且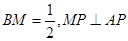 .
.
(1)求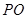 的长;
的长;
(2)求二面角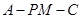 的正弦值.
的正弦值.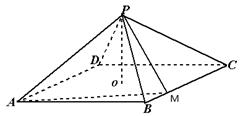
(1)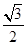 ;(2)
;(2)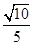 .
.
解析试题分析:(1)连结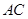 、
、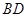 ,因为是菱形
,因为是菱形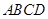 的中心,
的中心,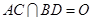 ,以
,以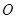 为坐标原点,
为坐标原点,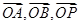 的方向分别为
的方向分别为 轴、
轴、 轴、
轴、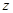 轴的正方向,建立空间直角坐标系,根据题设条件写出
轴的正方向,建立空间直角坐标系,根据题设条件写出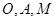 的坐标,并设出点
的坐标,并设出点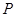 的坐标
的坐标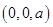 ,根据空间两点间的距离公式和勾股定理列方程解出
,根据空间两点间的距离公式和勾股定理列方程解出 的值得到
的值得到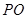 的长;.
的长;.
(2)设平面 的法向量为
的法向量为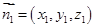 ,平面PMC的法向量为
,平面PMC的法向量为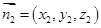 ,首先利用向量的数量积列方程求出向量
,首先利用向量的数量积列方程求出向量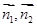 的坐标,再利用向量的夹角公式求出
的坐标,再利用向量的夹角公式求出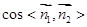 ,进而求出二面角
,进而求出二面角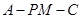 的正弦值.
的正弦值.
解: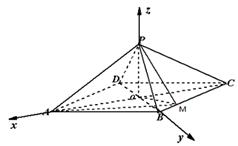
(1)如图,连结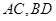 ,因
,因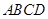 为菱形,则
为菱形,则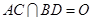 ,且
,且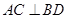 ,以
,以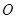 为坐标原点,
为坐标原点,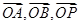 的方向分别为
的方向分别为 轴,
轴, 轴,
轴,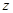 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系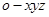 ,
,
因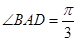 ,故
,故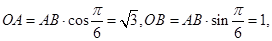
所以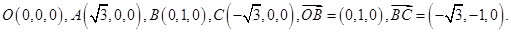
由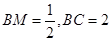 知,
知,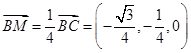
从而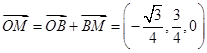 ,即
,即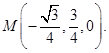
设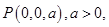 ,则
,则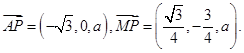 因为
因为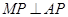 ,
,
故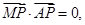 即
即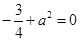 ,所以
,所以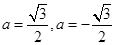 (舍去),即
(舍去),即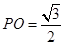 .
.
(2)由(1)知, ,
,
设平面 的法向量为
的法向量为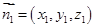 ,平面
,平面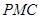 的法向量为
的法向量为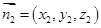
由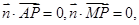 得
得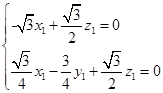 故可取
故可取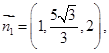
由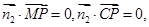 得
得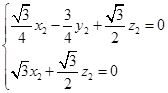 故可取
故可取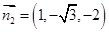
从而法向量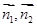 的夹角的余弦值为
的夹角的余弦值为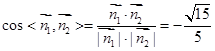
故所求二面角 的正弦值为
的正弦值为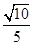 .
.
考点:1、空间直线与平面垂直的性质;2、空间直角坐标系;3、空间向量的数量积及其应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
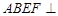 平面
平面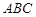 ,四边形
,四边形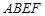 为矩形,
为矩形,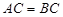 .
.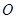 为
为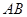 的中点,
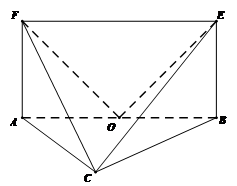
的中点,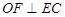 .
.
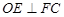 ;
;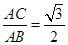 时,求二面角
时,求二面角 的余弦值.
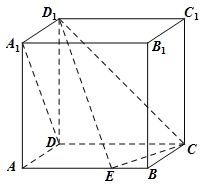
的余弦值.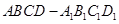 的所有棱长都相等,
的所有棱长都相等,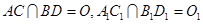 ,四边形
,四边形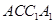 和四边形
和四边形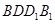 为矩形.
为矩形.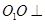 底面
底面 ;
;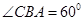 ,求二面角
,求二面角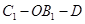 的余弦值.
的余弦值.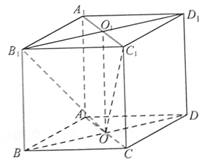
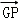 =λ
=λ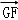 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为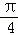 ,求λ的值.
,求λ的值.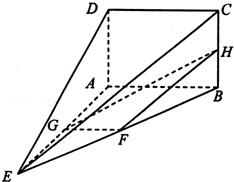
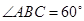 ,平面
,平面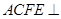 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.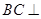 平面ACFE;
平面ACFE;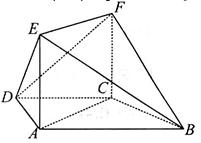
 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.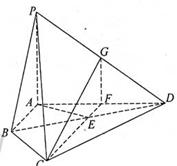
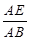 的值;
的值;