题目内容
设函数f(x)=cos(x+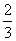 π)+2cos2
π)+2cos2
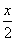 ,x∈R.
,x∈R.
(1)求f(x)的值域;
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若f(B)=1,b=1,c=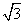 ,求a的值.
,求a的值.
解:(1)f(x)=cosxcos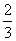 π-sinxsin
π-sinxsin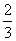 π+cosx+1
π+cosx+1
=- cosx-
cosx- sinx+cosx+1
sinx+cosx+1
= cos
cos x-
x- sinx+1=sin(x+
sinx+1=sin(x+ )+1,
)+1,
因此f(x)的值域为[0,2].
(2)由f(B)=1得sin(B+ )+1=1,即sin(B+
)+1=1,即sin(B+ )=0.
)=0.
又因为0<B<π,故B= .
.
法一:由余弦定理b2=a2+c2-2accosB,得a2-3a+2=0,解得a=1或a=2.
法二:由正弦定理 ,得sinC=
,得sinC= ,
,
所以C= 或C=
或C= .
.
当C= 时,A=
时,A= ,从而a=
,从而a= =2;
=2;
当C= 时,A=
时,A= ,又B=
,又B= ,从而a=b=1.
,从而a=b=1.
故a的值为1或2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =________.
=________. )在区间[-
)在区间[- ,π]上的简图是( )
,π]上的简图是( )
 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )
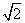 ,cosA=-
,cosA=-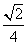 .
.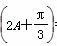 的值.
的值. 海里/时 B.34
海里/时 B.34 海里/时
海里/时 海里/时 D
海里/时 D .34
.34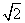 海里/时
海里/时 B.
B.
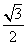 D.
D.


 1-an=2n,则
1-an=2n,则 的最小值为________.
的最小值为________. =
=
 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.