题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知a=2,c=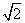 ,cosA=-
,cosA=-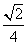 .
.
(1)求sinC和b的值;
(2)求cos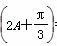 的值.
的值.
解:(1)在△ABC中,由cosA=-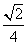 ,可得s
,可得s inA=
inA= .
.
又由 及a=2,c=
及a=2,c=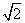 ,可得sinC=
,可得sinC= .
.
由a2=b2+c2-2bccosA,得b2+b-2=0,
因为b>0,故解得b=1.所以sinC= ,b=1.
,b=1.
(2)由cosA=-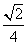 ,sinA=
,sinA= ,
,
得cos2A=2cos2A-1=- ,
,
sin2A=2sinAcosA=- .
.
所以,cos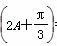 =cos2Acos
=cos2Acos -sin2Asin
-sin2Asin
= .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ,α是第三象限的角,则sin(α+
,α是第三象限的角,则sin(α+ )=( )
)=( )
 上单调递减,则ω的取值范围是( )
上单调递减,则ω的取值范围是( ) B.
B.
 D.(0,2]
D.(0,2]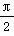 ,直线x=
,直线x=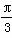 是其图象的一条对称轴,若A>0,ω>0,0<φ<
是其图象的一条对称轴,若A>0,ω>0,0<φ< B.
B.
 D.-
D.-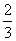 π)+2cos2
π)+2cos2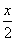 ,x∈R.
,x∈R.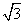 ,求a的值.
,求a的值.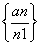 的前n项和的公式是(
的前n项和的公式是( )
)