题目内容
2.已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,圆C:x2+y2=6-a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1,椭圆M在点P处的切线斜率为k2,则$\frac{{k}_{1}}{{k}_{2}}$的取值范围为( )| A. | (1,6) | B. | (1,5) | C. | (3,6) | D. | (3,5) |
分析 由题意可知椭圆的焦点在x轴上,则$\left\{\begin{array}{l}{\sqrt{6-{a}^{2}}<a}\\{\sqrt{6-{a}^{2}}>1}\end{array}\right.$,求得3<a2<5,根据椭圆及圆的切线方程,求得切线的斜率,即可求得$\frac{{k}_{1}}{{k}_{2}}$=a2,求得$\frac{{k}_{1}}{{k}_{2}}$的取值范围.
解答  解:设P(x0,y0),
解:设P(x0,y0),
由椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,圆C:x2+y2=6-a2在第一象限有公共点P,
当焦点在x轴时,即a>1时,
则$\left\{\begin{array}{l}{\sqrt{6-{a}^{2}}<a}\\{\sqrt{6-{a}^{2}}>1}\end{array}\right.$,解得:3<a2<5,
当焦点在y轴,即0<a<1时,显然圆与椭圆无交点,
圆x2+y2=6-a2在P点的切线方程为x0x+y0y=6-a2,则切线斜率k1=-$\frac{{x}_{0}}{{y}_{0}}$,
椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+y2=1在P点的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+{y}_{0}y=1$,则切线斜率k2=-$\frac{{x}_{0}}{{y}_{0}{a}^{2}}$,
则$\frac{{k}_{1}}{{k}_{2}}$=a2,
∴$\frac{{k}_{1}}{{k}_{2}}$的取值范围(3,5),
故选:D.
点评 本题考查椭圆及圆的切线方程,考查圆与椭圆的交点问题,考查计算能力,属于难题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
14.已知函数满足一下两个条件:①任意x1,x2∈(0,+∞),且x1≠x2时,(x1-x2)[f(x1)-f(x2)]<0;②对定义域内任意x有f(x)+f(-x)=0,则符合条件的函数是( )
| A. | f(x)=2x | B. | f(x)=1-|x| | C. | $f(x)=\frac{1}{x}-x$ | D. | f(x)=ln(x+1) |
7.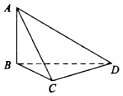 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
14.设集合M={-1,1},N={x|$\frac{1}{x}$<2},则下列结论正确的是( )
| A. | N⊆M | B. | M⊆N | C. | M∩N=N | D. | M∩N={1} |