题目内容
设函数f′（x）=x2+3x-4，则y=f（x）的单调减区间（ ）
| A、（-4，1） |
| B、（-∞，-4），（1，+∞） |
| C、（-∞，-4） |
| D、（1，+∞） |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：找使f′（x）＜0的x的取值，便能得到y=f（x）的单调减区间．
解答：
解：解x2+3x-4=0得：x=-4，或1；
∴x∈（-4，1）时f′（x）＜0；
∴函数y=f（x）在（-4，1）上单调递减，（-4，1）是它的单调减区间．
故选：A．
∴x∈（-4，1）时f′（x）＜0；
∴函数y=f（x）在（-4，1）上单调递减，（-4，1）是它的单调减区间．
故选：A．
点评：考查导数符号与函数单调性的关系．
练习册系列答案
名校课堂系列答案
相关题目
已知点P在直线AB上，点O不在直线AB上，且存在实数t满足
=2t
+t
，则
=（ ）
| OP |
| PA |
| OB |
|
| ||
|
|
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
函数f（x）=
+
的定义域是（ ）
| x-1 |
| 1 |
| x-2 |
| A、[1，+∞） |
| B、（2，+∞） |
| C、（1，2） |
| D、[1，2）∪（2，+∞） |
集合A={x∈R|ax2+ax+1=0}的子集只有2个，则a=（ ）
| A、4 | B、2 | C、0 | D、0或4 |
方程x
-（
）x-2=0的解所在的区间为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
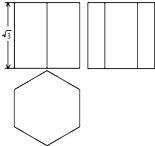如图是一个六棱柱的三视图，俯视图是一个周长为3的正六边形，该六棱柱的顶点都在同一个球面上，那么这个球的体积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
，若f（a）=4，则实数a=（ ）
|
| A、-2或6 | ||
B、-2或
| ||
| C、-2或2 | ||
D、2或
|