题目内容

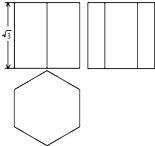如图是一个六棱柱的三视图，俯视图是一个周长为3的正六边形，该六棱柱的顶点都在同一个球面上，那么这个球的体积为（　　）
A、
π
2
B、
4π
3
C、
5π
3
D、
π
3
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：先求正六棱柱的体对角线，就是外接球的直径，然后求出球的体积．
解答： 解：正六边形周长为3，得边长为
1
2
，故其主对角线为1，
从而球的直径2R=2，
∴R=1，
∴球的体积V=
4π
3
．
故答案为：
4π
3
．
点评：本题考查球的体积，解题的关键是确定球的直径，属于基础题．
练习册系列答案
相关题目
已知全集U={1，2，3，4，5}，A={1，2，4}，B={2，3}，则（∁UA）∩B=
 
．
设函数f′（x）=x2+3x-4，则y=f（x）的单调减区间（　　）
A、（-4，1）
B、（-∞，-4），（1，+∞）
C、（-∞，-4）
D、（1，+∞）
对总数为N的一批零件用简单随机抽样方法抽取一个容量为30的样本，若每个零件被抽到的概率为0.25，则N的值为（　　）
A、100B、120
C、150D、200
若在直角坐标平面内A，B两点满足条件：
①点A，B都在函数y=f（x）的图象上；
②点A，B关于原点对称，则称A，B为函数y=f（x）的一个“黄金点对”．
那么函数f（x）=
x2+2x-2(x≤0)
1
x
(x＞0)
的“黄金点对”的个数是（　　）
A、0个B、1个C、2个D、3个
已知tanα=-
1
2
，则
(sinα-cosα)2
cos2α
的值为（　　）
A、2B、-2C、3D、-3
下列函数中既不是奇函数，又不是偶函数的是（　　）
A、y=2|x|
B、y=2x+2-x
C、y=lg
1
x+1
D、y=lg（x+
x2+1
）
若⊙O1与⊙O2相切，且O1O2=5，⊙O1的半径r1=2，则⊙O2的半径r2是（　　）
A、3B、5C、7D、3或7
已知函数f（x）=
1
2
x2-ax+（a-1）lnx，求函数f（x）的极值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网