题目内容
甲、乙两位同学约定晚饭6点到7点之间在食堂见面,先到之人等后到之人十五分钟,则甲、乙两人能见面的概率为 .
考点:几何概型
专题:概率与统计
分析:由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|6<x<7,6<y<7},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|6<x<7,8<y<7,0<x-y<
,0<y-x<
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:由题意知,如图: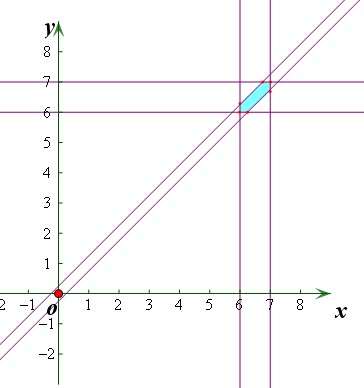
试验包含的所有事件是Ω={(x,y)|6<x<7,6<y<7},
事件对应的集合表示的面积是s=1,
阴影部分是满足条件的事件A={(x,y)|6<x<7,8<y<7,0<x-y<
,0<y-x<
},
∵(图中阴影部分)表示的面积是1-2×
×(1-
)2=
根据几何概型概率公式得到P=
,
故答案为:
.

试验包含的所有事件是Ω={(x,y)|6<x<7,6<y<7},
事件对应的集合表示的面积是s=1,
阴影部分是满足条件的事件A={(x,y)|6<x<7,8<y<7,0<x-y<
| 1 |
| 4 |
| 1 |
| 4 |
∵(图中阴影部分)表示的面积是1-2×
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 16 |
根据几何概型概率公式得到P=
| 7 |
| 16 |
故答案为:
| 7 |
| 16 |
点评:本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
复数z=cos120°+isin120°,则z3=( )
A、
| ||||||
B、-
| ||||||
C、
| ||||||
| D、1 |
函数f(x)=
在[2,+∞)上为增函数,且f(0)=0,则f(x)的最小值是( )
|
|
| A、f(2) | B、f(0) |
| C、f(-2) | D、f(4) |
“函数f(x)=x2+2x+m存在零点”的一个必要不充分条件是( )
| A、m≤1 | B、m≤2 |
| C、m≤0 | D、1≤m≤2 |
