题目内容
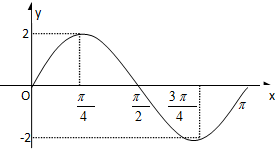已知函数f（x）=Asin2x（A＞0）的部分图象如图所示．（1）判断函数y=f（x）在区间[
| π |
| 4 |
| 3π |
| 4 |
（2）求函数y=f（x）的周期T．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）通过函数的图象直接判断函数的单调性，找出函数的最大值即可．
（2）利用函数的解析式直接通过函数的周期公式求解函数的周期即可．
（2）利用函数的解析式直接通过函数的周期公式求解函数的周期即可．
解答：
（本小题满分6分）
解：（1）由函数的图象可知，x=
时，函数取得最大值，x=
时，函数取得最小值，
∴函数y=f（x）在区间[
，
]上是减函数，且最大值为2；…（3分）
（2）由函数f（x）=Asin2x（A＞0）
∴周期T=
=
=π．…（6分）
（本小题满分6分）解：（1）由函数的图象可知，x=
| π |
| 4 |
| 3π |
| 4 |
∴函数y=f（x）在区间[
| π |
| 4 |
| 3π |
| 4 |
（2）由函数f（x）=Asin2x（A＞0）
∴周期T=
| 2π |
| |ω| |
| 2π |
| 2 |
点评：本题考查三角函数的图象的应用，函数的基本性质：单调性与最大值、周期的求法，考查视图用图能力．
练习册系列答案
百年学典课时学练测系列答案
相关题目
已知集合A、B均为集合U={1，2，3，4}的子集，A∩B={1}，A∪B={1，2，4}，则A=（ ）
| A、{1} |
| B、{1，2} |
| C、{1，2，3} |
| D、{1，2，4} |
在样本数据的回归分析中，相关指数R2的值越大，则残差平方和
(yi-
i)2（ ）
| n |
 |
| i=1 |
| ? |
| y |
| A、越小 | B、越大 |
| C、可能大也可能小 | D、以上都不对 |