题目内容
已知点P是圆x2+y2=4上的动点,过点P作PD⊥x轴,垂足为D,点M在DP的延长线上,且DM:DP=3:2;求点M的轨迹方程.
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:设出M点的坐标,由DM:DP=3:2得到P点的坐标,把P的坐标代入圆x2+y2=4,整理后去掉曲线与x轴的交点得答案.
解答:
解:设M(x,y),
由DM:DP=3:2,得P(x,
),
又∵点P在圆x2+y2=4上,
∴x2+(
)2=4.
∵D坐标为(x,0),当x=±2时,P点和D点坐标相同,即两点重合,此时约束条件中DP垂直于x轴没有意义,
故x=±2舍去.
∴M的轨迹方程是:
+
=1(x=±2).
由DM:DP=3:2,得P(x,
| 2y |
| 3 |
又∵点P在圆x2+y2=4上,
∴x2+(
| 2y |
| 3 |
∵D坐标为(x,0),当x=±2时,P点和D点坐标相同,即两点重合,此时约束条件中DP垂直于x轴没有意义,
故x=±2舍去.
∴M的轨迹方程是:
| x2 |
| 4 |
| y2 |
| 9 |
点评:本题考查了轨迹方程,训练了利用代入法求曲线方程,此题往往漏除曲线与x轴的交点,属中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
若复数z=i+i2014,则复数
+
(i为虚数单位)在复平面内对应的点所在象限为( )
. |
| z |
| 10 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某学员在一次射击测试中射靶10次,命中环数如:7,8,7,9,5,4,9,10,7,4则平均命中环数和命中环数的标准差为( )
| A、7,2 | B、7,4 |
| C、6,2 | D、6,4 |
若定义域为区间(-2,-1)的函数f(x)=log(2a-3)(x+2),满足f(x)<0,则实数a的取值范围是( )
A、(
| ||
| B、(2,+∞) | ||
C、(
| ||
D、(1,
|
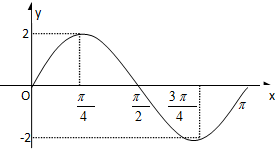 已知函数f(x)=Asin2x(A>0)的部分图象如图所示.
已知函数f(x)=Asin2x(A>0)的部分图象如图所示.