题目内容
设函数f（x）=x+
+b（a＞b＞0），求f（x）的单调区间，并证明f（x）在其单调区间上的单调性．
| a |
| x |
考点：函数单调性的性质
专题：函数的性质及应用,导数的概念及应用
分析：利用导数求函数的单调区间，并用定义证明其单调性．
解答：
解：∵f（x）=x+
+b（a＞b＞0
∴f′（x）=1-
则由1-
≥0得x≤-
或x≥
，故函数f（x）的递增区间是（-∞，-
]，[
，+∞）；
由1-
≤0得，-
≤x≤
，又x≠0，故函数f（x）的递减区间是[-
，0），（0，
]．
下面证明f（x）在（0，
]上是减函数：
证明：设任意的x1，x2∈（0，
]，且x1＜x2，则
f（x1）-f（x2）=（x1-x2）•
∵x1，x2∈（0，
]，且x1＜x2，
∴x1-x2＜0，x1x2＞a，x1x2＞0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴f（x）在（0，
]上是减函数．
同理可证f（x）在[-
，0）上是减函数，在（-∞，-
]，[
，+∞）上是增函数．
| a |
| x |
∴f′（x）=1-
| a |
| x2 |
| a |
| x2 |
| a |
| a |
| a |
| a |
由1-
| a |
| x2 |
| a |
| a |
| a |
| a |
下面证明f（x）在（0，
| a |
证明：设任意的x1，x2∈（0，
| a |
f（x1）-f（x2）=（x1-x2）•
| x1x2-a |
| x1x2 |
∵x1，x2∈（0，
| a |
∴x1-x2＜0，x1x2＞a，x1x2＞0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴f（x）在（0，
| a |
同理可证f（x）在[-
| a |
| a |
| a |
点评：考查了利用导数求函数单调区间的方法，以及用函数单调性的定义证明函数的增减性的方法，属常规题目．
练习册系列答案
相关题目
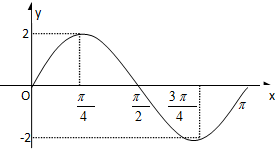已知函数f（x）=Asin2x（A＞0）的部分图象如图所示．