题目内容
以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[-M,M].例如,当φ1(x)=x3,φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”?“?b∈R,?x∈R,f(a)=b”;
②若函数f(x)∈B,则f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)∉B;
④若函数f(x)=
(a∈R),则f(x)∈B.
其中的真命题有 .(写出所有真命题的序号).
①设函数f(x)的定义域为D,则“f(x)∈A”?“?b∈R,?x∈R,f(a)=b”;
②若函数f(x)∈B,则f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)∉B;
④若函数f(x)=
| ax |
| x2+1 |
其中的真命题有
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据题中的新定义,结合函数值域的概念,可判断出命题①②③是否正确,再利分类讨论④中函数的值域,可得到其真假情况,从而得到本题的结论.
解答:
解:(1)对于命题①
“f(x)∈A”即函数f(x)值域为R,
“?b∈R,?a∈D,f(a)=b”表示的是函数可以在R中任意取值,
故有:设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“?b∈R,?a∈D,f(a)=b”
∴命题①是真命题;
(2)对于命题②
若函数f(x)∈B,即存在一个正数M,使得函数f(x)的值域包含于区间[-M,M].
∴-M≤f(x)≤M.例如:函数f(x)满足-2<f(x)<5,则有-5≤f(x)≤5,此时,f(x)无最大值,无最小值.
∴命题②“函数f(x)∈B的充要条件是f(x)有最大值和最小值.”是假命题;
(3)对于命题③
若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,
则f(x)值域为R,f(x)∈(-∞,+∞),
并且存在一个正数M,使得-M≤g(x)≤M.
∴f(x)+g(x)∈R.
则f(x)+g(x)∉B.
∴命题③是真命题.
(4)对于命题④∵函数f(x)=
当x=0时,f(x)=0,
当x>0时,x+
≥2,
∴0<
≤
,
当a=0时,f(x)=0,
当a>0时,0<f(x)≤
,
当a<0时,
≤f(x)<0,
当x<0时,x+
≤-2,
-
≤
<0
当a=0时,f(x)=0,
当a>0时,-
≤<f(x)<0,
当a<0时,0<<f(x)≤-
,
综上所述即,f(x)∈B.
故命题④是真命题.
故答案为①③④.
“f(x)∈A”即函数f(x)值域为R,
“?b∈R,?a∈D,f(a)=b”表示的是函数可以在R中任意取值,
故有:设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“?b∈R,?a∈D,f(a)=b”
∴命题①是真命题;
(2)对于命题②
若函数f(x)∈B,即存在一个正数M,使得函数f(x)的值域包含于区间[-M,M].
∴-M≤f(x)≤M.例如:函数f(x)满足-2<f(x)<5,则有-5≤f(x)≤5,此时,f(x)无最大值,无最小值.
∴命题②“函数f(x)∈B的充要条件是f(x)有最大值和最小值.”是假命题;
(3)对于命题③
若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,
则f(x)值域为R,f(x)∈(-∞,+∞),
并且存在一个正数M,使得-M≤g(x)≤M.
∴f(x)+g(x)∈R.
则f(x)+g(x)∉B.
∴命题③是真命题.
(4)对于命题④∵函数f(x)=
| ax |
| x2+1 |
当x=0时,f(x)=0,
当x>0时,x+
| 1 |
| x |
∴0<
| 1 | ||
x+
|
| 1 |
| 2 |
当a=0时,f(x)=0,
当a>0时,0<f(x)≤
| a |
| 2 |
当a<0时,
| a |
| 2 |
当x<0时,x+
| 1 |
| x |
-
| 1 |
| 2 |
| 1 | ||
x+
|
当a=0时,f(x)=0,
当a>0时,-
| a |
| 2 |
当a<0时,0<<f(x)≤-
| a |
| 2 |
综上所述即,f(x)∈B.
故命题④是真命题.
故答案为①③④.
点评:本题考查了函数值域的概念、基本不等式、充要条件,还考查了新定义概念的应用和极限思想.本题计算量较大,也有一定的思维难度,属于难题.

练习册系列答案
相关题目
已知命题p:f(x)=
e-x在(0,+∞)上单调递减;命题q:双曲线
-
=1的焦点到抛物线x2=
y的准线的距离为2,则下列命题正确的是( )
| 1 | ||
|
| x2 |
| 4 |
| y2 |
| 5 |
| 1 |
| 4 |
| A、p∨q | B、p∧q |
| C、¬p∧q | D、¬p∨q |
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、18π | ||
| D、20π |
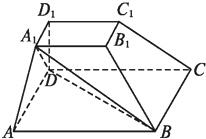 如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.