题目内容
14.C${\;}_{5n}^{11-2n}$-A${\;}_{11-3n}^{2n-2}$=100.分析 根据题意,结合排列数、组合数的性质可得$\left\{\begin{array}{l}{11-2n≤5n}\\{2n-2≤11-3n}\\{11-2n≥0}\\{2n-2≥0}\end{array}\right.$,解可得n的范围,又由n是正整数,可得n的值,将n的值代入C${\;}_{5n}^{11-2n}$-A${\;}_{11-3n}^{2n-2}$中,计算可得答案.
解答 解:根据题意,对于C${\;}_{5n}^{11-2n}$-A${\;}_{11-3n}^{2n-2}$,
有$\left\{\begin{array}{l}{11-2n≤5n}\\{2n-2≤11-3n}\\{11-2n≥0}\\{2n-2≥0}\end{array}\right.$,
解可得$\frac{11}{7}$≤n≤$\frac{13}{5}$,
又由n是正整数,则n=2,
则C${\;}_{5n}^{11-2n}$-A${\;}_{11-3n}^{2n-2}$=${C}_{10}^{7}$-${A}_{5}^{2}$=120-20=100;
故答案为:100.
点评 本题考查排列、组合数公式的应用,关键是利用排列、组合的公式求出n的值.

练习册系列答案
相关题目
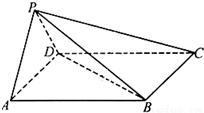 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.