题目内容
8.高斯函数f(x)=[x]的函数值表示不超过x的最大整数,如[-2.3]=-3,[1.2]=1.设函数g(x)=x-f(x),函数u(x)={sinπx},则下列说法正确的是( )| A. | 函数g(x)与u(x)的值域相同 | B. | 函数g(x)与u(x)的最小正周期相同 | ||
| C. | 函数g(x)与u(x)的单调区间相同 | D. | 函数g(x)与u(x)奇偶性相同 |
分析 由题意,函数f(x)=[x]的函数值表示不超过x的最大整数,这个整数必须是小于等于x的最大整数,g(x)=x-f(x),可得0≤g(x)<1,函数u(x)={sinπx}={1,0,-1}.可得答案.
解答 解:由题意,函数f(x)=[x]的函数值表示不超过x的最大整数,这个整数必须是小于等于x的最大整数,函数f(x)=x-[x],则f(-x)=-x-[-x]
例如f(3.5)=3.5-[3.5]=3.5-3=0.5,而f(-3.5)=-3.5-[-3.5]=-3.5+4=0.5=f(3.5),则函数是偶函数;
g(x+1)=x+1-[x+1]=g(x)=x-[x];∴g(x+1)=g(x).是周期T=1的函数.∴0≤g(x)<1,
函数u(x)={sinπx}={1,0,-1},是奇函数,
综上分析,可得函数g(x)与u(x)的单调区间相同,
故选C.
点评 本题主要考查了对新定义的充分理解和认识,求解函数的值域问题,已知“函数f(x)=[x]的函数值表示不超过x的最大整数”的含义是解题的关键

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
18.已知平面向量$\overrightarrow{AB}$=(1,2),$\overrightarrow{AC}$=(3,4),则向量$\overrightarrow{CB}$=( )
| A. | (-4,-6) | B. | (4,6) | C. | (-2,-2) | D. | (2,2) |
3.命题p:方程$\frac{x^2}{m-5}-\frac{y^2}{m+3}=1$表示双曲线的充要条件是-3<m<5;
命题q:存在x0∈R,使得sinx0-cosx0=2,则( )
命题q:存在x0∈R,使得sinx0-cosx0=2,则( )
| A. | 命题“p或q”是假命题 | B. | 命题“p且q”是真命题 | ||
| C. | 命题“非q”是假命题 | D. | 命题“p且‘非q’”是真命题 |
13.在一个口袋中装5个白球和3个黑球,这些球除颜色外完全相同,从中摸出1个球,则摸到黑球的概率是( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
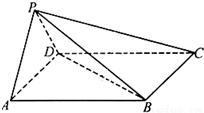 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.