题目内容
已知f(x)=x3-3x+m+2,在[0,2]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边的三角形,则实数m的范围是( )
| A、m>2 | B、m>4 |
| C、m>6 | D、m>8 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出函数的导数,知道x在[0,2]内,函数先减小后增加,计算两端及最小值,根据三角形三边之间的关系,从而求出实数m的范围.
解答:
解:f(x)=x3-3x+m+2,
求导f'(x)=3x2-3,由f'(x)=0得到x=1或x=-1,
知道x在[0,2]内,函数先减小后增加,
计算两端及最小值
f(0)=m+2,f(2)=4+m,f(1)=m,
在[0,2]上任取三个数A,B,C,均存在以f(a),f(b),f(c)为边的三角形
由题意知,f(1)=m>0 (1)
f(1)+f(1)>f(0),得到2m>m+2 (2)
f(1)+f(1)>f(2),得到2m>4+m (3)
由(1)(2)(3)得到m>4为所求,
故选:B.
求导f'(x)=3x2-3,由f'(x)=0得到x=1或x=-1,
知道x在[0,2]内,函数先减小后增加,
计算两端及最小值
f(0)=m+2,f(2)=4+m,f(1)=m,
在[0,2]上任取三个数A,B,C,均存在以f(a),f(b),f(c)为边的三角形
由题意知,f(1)=m>0 (1)
f(1)+f(1)>f(0),得到2m>m+2 (2)
f(1)+f(1)>f(2),得到2m>4+m (3)
由(1)(2)(3)得到m>4为所求,
故选:B.
点评:本题考查了函数的单调性,导数的应用,考查三角形三边之间的关系,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
二项式(1+x)n展开式的二项式系数之和为64,则(1-2x)n展开式第四项的系数为( )
| A、20 | B、-160 |
| C、160 | D、-20 |
如图,在正方体ABCD-A1B1C1D1中,异面直线AD1与BA1所成的角为( )
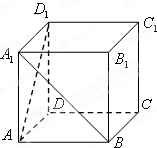

| A、30° | B、45° |
| C、60° | D、90° |
已知复数z1=1-i,z2=1+i,则
等于( )
| z1-z2 |
| i |
| A、2i | B、-2 |
| C、2+i | D、-2+i |

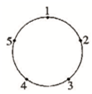 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按顺时针方向绕圆从一个点跳到另一点;若停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次可以跳两个点,该青蛙从5这点跳起,跳2008次后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按顺时针方向绕圆从一个点跳到另一点;若停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次可以跳两个点,该青蛙从5这点跳起,跳2008次后它将停在的点是( )