题目内容
2．已知全集U=R，A={x|-2≤x≤4}，B={x|-3≤x≤3}，求（∁UA）∩（∁UB）=（ ）| A． | {x|-2≤x≤3} | B． | {x|x＜-2或x＞4} | C． | {x|-3≤x≤4} | D． | {x|x＜-3或x＞4} |
分析 利用集合的交、并、补集的运算，可求得A∪B，再利用（∁UA）∩（∁UB）=∁U（A∪B）即可求得答案．
解答 解：∵A={x|-2≤x≤4}，B={x|-3≤x≤3}，
∴A∪B═{x|-3≤x≤4}，
∴（∁UA）∩（∁UB）=∁U（A∪B）={x|x＜-3或x＞4}，
故选：D．
点评 本题考查交、并、补集的混合运算，解答中运用了“摩根定律”：（∁UA）∩（∁UB）=∁U（A∪B），（∁UA）∪（∁UB）=∁U（A∩B），属于基础题．
练习册系列答案
相关题目
10．已知圆M过三点A（0，0），B（1，1），C（4，2），过点D（-1，4）作圆M的两条切线，两切点分别为E，F，
（I） 求圆M的方程．
（II） 求切线DE，DF方程
（ III）求直线EF的方程．
（I） 求圆M的方程．
（II） 求切线DE，DF方程
（ III）求直线EF的方程．
14．已知函数f（x）=$\left\{\begin{array}{l}{kx-1，x≤0}\\{{2}^{-x}-1，x＞0}\end{array}\right.$，（k＜0），当方程f[f（x）]=-$\frac{1}{2}$恰有三个实数根时，实数k的取值范围为（ ）
| A． | （-$\frac{1}{2}$，0） | B． | [-$\frac{1}{2}$，0） | C． | （-∞，-$\frac{1}{2}$] | D． | （-∞，-$\frac{1}{2}$） |
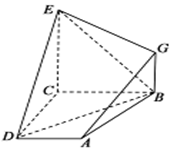如图，已知四边形BCD和BCEG均为直角梯形，AD∥EG、CE∥BG，且∠BCD=∠BCE=$\frac{π}{2}$，平面ABCD⊥平面BCEG，BC=2AD，CE=2BG．求证：