题目内容
已知函数f（x）=log
（4x-2x+1+1）的值域是[0，+∞），则它的定义域可以是（ ）
| 1 |
| 2 |
| A、（0，1] |
| B、（0，1） |
| C、（-∞，1] |
| D、（-∞，0] |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据对数函数的性质即可得到结论．
解答：
解：∵函数f（x）=log
（4x-2x+1+1）的值域是[0，+∞），
∴设t=2x，则y=4x-2x+1+1=t2-2t+1=（t-1）2．
则只要保证y=（t-1）2∈（0，1]，即可，
故当x∈（0，1]，满足条件，
故选：A
| 1 |
| 2 |
∴设t=2x，则y=4x-2x+1+1=t2-2t+1=（t-1）2．
则只要保证y=（t-1）2∈（0，1]，即可，
故当x∈（0，1]，满足条件，
故选：A
点评：本题主要考查函数的定义域和值域的应用，利用换元法是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=ax+loga（x+1）在[0，1]上的最大值与最小值之和为a，则a的值为（ ）
A、
| ||
| B、2 | ||
| C、4 | ||
D、
|
下列函数中既是奇函数，又在区间（-1，1）上是增函数的为（ ）
| A、y=ex+e-x |
| B、y=|x| |
| C、y=sinx |
| D、y=-x3 |
函数y=
的定义域是（ ）
| 1 | ||
|
| A、（1，+∞） |
| B、R |
| C、（-∞，1）∪（1+∞） |
| D、（-∞，1） |
已知集合A={x|x=
，k∈N}，B={x|x≤4，x∈Q}，则A∩B为（ ）
| 2k+1 |
| A、{0，3} |
| B、{1，3} |
| C、{1，4} |
| D、{1，2，3，4} |
若方程2x2+4x+1=0，则|x2-x1|=（ ）
A、-
| ||
B、±
| ||
C、
| ||
| D、0 |
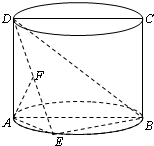如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上（点E异于A、B两点），点F在DE上，且AF⊥DE，若圆柱的底面积与△ABE的面积之比等于π．