题目内容
直线x+m2y+6=0与直线(m-2)x+3my+2m=0没有公共点,则m的值是 .
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:利用两直线平行的性质求解.
解答:
解:∵直线x+m2y+6=0与直线(m-2)x+3my+2m=0没有公共点,
∴
=
≠
,或m=0
解得-1或m=0.
故答案为:-1或0.
∴
| m-2 |
| 1 |
| 3m |
| m2 |
| 2m |
| 6 |
解得-1或m=0.
故答案为:-1或0.
点评:本题考查实数值的求法,是基础题,解题时要注意两直线平行的条件的灵活运用.

练习册系列答案
相关题目
已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则tanθ=( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
已知直线a、b,平面α、β,那么下列命题中正确的是( )
| A、若a⊥b,b⊥α,则a∥α |
| B、若a?α,b?β,a∥b,则α∥β |
| C、若a∥α,a⊥b,则b⊥α |
| D、若a∥α,a⊥β,则α⊥β |
若a>0,b>0,a+b=2,给出下列四个结论:①ab≤1②
+
≤
③a2+b2≥2④
+
≥2,其中所有正确结论的序号是( )
| a |
| b |
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、①② | B、②③④ |
| C、③④ | D、①③④ |
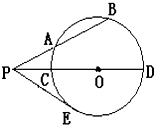 如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7
如图,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,PE是⊙O的切线.已知PA=6,AB=7