题目内容
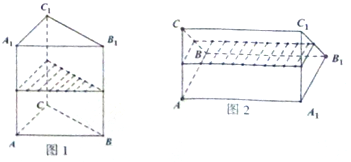
如图1，一个正三棱柱容器，底面边长为a，高为2a，内装水若干，将容器放倒，把一个侧面作为底面，如图2，这时水面恰好为中截面，则图1容器中水面的高度是 ．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：先求出图2中水的体积，通过谁的体积相等，即可求出图1中水的高度即可．
解答：
解：正三棱柱的底面积为S=
a2，图2中水的体积．
V水=V柱-VCEF-C1GH=S•2a-（
S）•2a=
aS．
设图1中水面的高度为x，则S•x=
aS，得x=
a．
故答案为：
a．
解：正三棱柱的底面积为S=
| ||
| 4 |
V水=V柱-VCEF-C1GH=S•2a-（
| 1 |
| 4 |
| 3 |
| 2 |
设图1中水面的高度为x，则S•x=
| 3 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查棱柱的体积，考查学生的转化思想，空间想象能力，是中档题．
练习册系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
如图，圆O上一点C在直径AB上的射影为D．AD=2，AC=2PT切⊙O于T，割线PAB经过O点交⊙O于A、B，若PT=4，PA=2，则cos∠BPT=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若ξ～B（10，
），则p（ξ≥2）等于（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|