题目内容
已知命题p：“椭圆
+
=1的焦点在x轴上”，命题q：只有一个实数x满足不等式x2+2ax+2a≤0．若命题“p或q”是假命题，求实数a的取值范围．
| x2 |
| 5 |
| y2 |
| a |
考点：复合命题的真假
专题：简易逻辑
分析：命题p：“椭圆
+
=1的焦点在x轴上”，可得0＜a＜5；命题q：只有一个实数x满足不等式x2+2ax+2a≤0．可得△=0；若命题“p或q”是假命题，则p与q都为假命题．
| x2 |
| 5 |
| y2 |
| a |
解答：
解：若命题P为真，则0＜a＜5，
若命题q为真，则△=4a2-8a=0，解得a=0或a=2．
当p或q为真命题时，则0≤a＜5．
命题“p或q”是假命题，
∴a的取值范围为a＜0或a≥5．
若命题q为真，则△=4a2-8a=0，解得a=0或a=2．
当p或q为真命题时，则0≤a＜5．
命题“p或q”是假命题，
∴a的取值范围为a＜0或a≥5．
点评：本题考查了简易逻辑的判定、椭圆的标准方程、一元二次不等式与判别式的关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中，定义域是（0，+∞）的函数是（ ）
| A、y=x3 | ||
B、y=x
| ||
C、y=x-
| ||
D、y=x
|
双曲线
-
=1的渐近线与圆（x-3）2+y2=r2（r＞0）相切，则r等于（ ）
| x2 |
| 12 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线C：
-
=1的焦距为10，点P（1，2）在C的渐近线上，则C的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在建立两个变量y与x的回归模型中，分别选择了4个不同模型，模型1-4的R2分别为0.98，0.80，0.50，0.25，则其中拟合得最好的模型是（ ）
| A、模型1 | B、模型2 |
| C、模型3 | D、模型4 |
已知某空间几何体的三视图如图所示，则（ ）
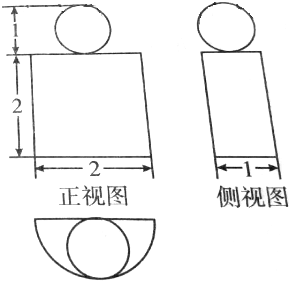
| A、该几何体的表面积为4+2π | ||
B、该几何体的体积为
| ||
| C、该几何体的表面积为4+4π | ||
| D、该几何体的体积为π |
已知实数x，y满足
，若可行域内存在点使得x+2y-a=0成立，则a的最大值为（ ）
|
| A、-1 | B、1 | C、4 | D、5 |