题目内容
请写出求二元一次方程组
（a1b2-a2b1≠0）的解的算法步骤，并画出相应的程序框图．
|
考点：程序框图
专题：图表型,算法和程序框图
分析：根据加法消元法，求出二元一次方程组
（a1b2-a2b1≠0）的解，根据求解过程，可得所求框图．
|
解答：
解：（I）算法步骤：
第一步，输入a1，b2，a2，b1，c1，c2，
第二步，计算x=
，
第三步，计算y=
，
第四步，输出x，y．
此问（6分），其中x，y表达式正确，各（2分），输入和输出部分，各（1分）
（II）程序框图
说明：此问不设步骤分，只有0分和（6分）．
第一步，输入a1，b2，a2，b1，c1，c2，
第二步，计算x=
| b2c1-b1c2 |
| a1b2-a2b1 |
第三步，计算y=
| a1c2-a2c1 |
| a1b2-a2b1 |
第四步，输出x，y．
此问（6分），其中x，y表达式正确，各（2分），输入和输出部分，各（1分）
（II）程序框图
说明：此问不设步骤分，只有0分和（6分）．
点评：本题考查的知识点是设计程序框图，解决实际问题，属于基础题．
练习册系列答案
优等生题库系列答案
相关题目
不等式ax2-（a+2）x+2≥0（a＜0）的解集为（ ）
A、[
| ||
B、[1，
| ||
C、(-∞，
| ||
D、(-∞，1]∪[
|
函数f（x）=2sin（
-x）是（ ）
| π |
| 2 |
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为4π的偶函数 |
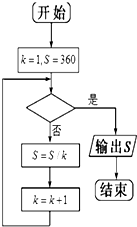执行如图所示的程序框图，运行的结果为S=3，那么判断框中应填入的关于k的判断条件是（ ）| A、k＞6？ | B、k＜6？ |
| C、k＞5？ | D、k＜5？ |