题目内容
角α的终边上有一点P(m,5),且cosα=
,m≠0,求sinα+cosα.
| m |
| 13 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由题意可得 x=m,y=5,m2+52=132,求得m2的值,可得 r=|OP|=13,再由 sinα=
,求得结果.
| y |
| r |
解答:
解:∵角α的终边上有一点P(m,5),且cosα=
,∴x=m,y=5,m2+52=132,
∴m2=12,∴r=|OP|=13.
由以上可得 sinα=
=
,cosα=
,
∴sinα+cosα=
+
=
.
| m |
| 13 |
∴m2=12,∴r=|OP|=13.
由以上可得 sinα=
| y |
| r |
| 5 |
| 13 |
| 12 |
| 13 |
∴sinα+cosα=
| 5 |
| 13 |
| 12 |
| 13 |
| 17 |
| 13 |
点评:本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知实数x,y满足
,则z=-x2-y的最小值是( )
|
| A、-8 | B、-2 | C、-1 | D、0 |
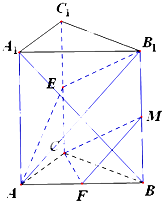 如图直三棱柱ABC-A1B1C1,CA=CB,E、F、M分别是棱CC1、AB、BB1中点.
如图直三棱柱ABC-A1B1C1,CA=CB,E、F、M分别是棱CC1、AB、BB1中点.


