题目内容
已知函数f(x)=ax2+2x+c,(a,c∈N*)满足①f(1)=5;②6<f(2)<11.
(1)求函数f(x)的解析表达式;
(2)若对任意x∈[1,2],都有f(x)-2mx≥1成立,求实数m的取值范围.
(1)求函数f(x)的解析表达式;
(2)若对任意x∈[1,2],都有f(x)-2mx≥1成立,求实数m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)f(1)=5可得c=3-a.①,由6<f(2)<11,得6<4a+c+4<11,②联立①②可求得a,c,进而可得函数f(x)的解析表达式;
(2)法一:设g(x)=f(x)-2mx-1=x2-2(m-1)x+1,x∈[1,2],则由已知得:当m-1≤1即m≤2时,gmin(x)=g(1)=4-2m≥0,解得m的取值范围.
(2)法二:不等式f(x)-2mx≥1恒成立等价于2m-2≤x+
在[1,2]上恒成立.只需求出(x+
)min.
(2)法一:设g(x)=f(x)-2mx-1=x2-2(m-1)x+1,x∈[1,2],则由已知得:当m-1≤1即m≤2时,gmin(x)=g(1)=4-2m≥0,解得m的取值范围.
(2)法二:不等式f(x)-2mx≥1恒成立等价于2m-2≤x+
| 1 |
| x |
| 1 |
| x |
解答:
解:(1)∵f(1)=5
∴5=a+c+2,即c=3-a,
又∵6<f(2)<11
∴6<4a+c+4<11,
∴∴-
<a<
,
又∵a∈N*,
∴a=1,c=2.
所以f(x)=x2+2x+2.
(2)法一:设g(x)=f(x)-2mx-1=x2-2(m-1)x+1,x∈[1,2],则由已知得:
当m-1≤1即m≤2时,gmin(x)=g(1)=4-2m≥0,此时m≤2;
当1<m-1<2即2<m<3时,△≤0,解得:无解;
当m-1≥2即m≥3时,gmin(x)=g(2)=9-4m≥0,此时无解.
综上所述,m的取值范围为(-∞,2].
法二:由已知得,2(m-1)≤x+
在x∈[1,2]上恒成立.
由于x+
在[1,2]上单调递增,
所以x+
∈[2,
],
故2(m-1)≤2,
即m≤2.
∴5=a+c+2,即c=3-a,
又∵6<f(2)<11
∴6<4a+c+4<11,
∴∴-
| 1 |
| 3 |
| 4 |
| 3 |
又∵a∈N*,
∴a=1,c=2.
所以f(x)=x2+2x+2.
(2)法一:设g(x)=f(x)-2mx-1=x2-2(m-1)x+1,x∈[1,2],则由已知得:
当m-1≤1即m≤2时,gmin(x)=g(1)=4-2m≥0,此时m≤2;
当1<m-1<2即2<m<3时,△≤0,解得:无解;
当m-1≥2即m≥3时,gmin(x)=g(2)=9-4m≥0,此时无解.
综上所述,m的取值范围为(-∞,2].
法二:由已知得,2(m-1)≤x+
| 1 |
| x |
由于x+
| 1 |
| x |
所以x+
| 1 |
| x |
| 5 |
| 2 |
故2(m-1)≤2,
即m≤2.
点评:本题考查二次函数的性质、二次不等式恒成立,考查转化思想,属中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知直线m,n,l,若m∥n,n∩l=P,则m与l的位置关系是( )
| A、异面直线 |
| B、相交直线 |
| C、平行直线 |
| D、相交直线或异面直线 |
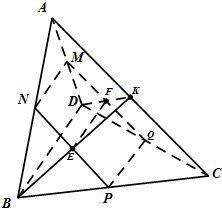 三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.
三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.