题目内容
设数列{an}是公比为q的等比数列,它的前n项和为Sn,若
Sn=2,则此等比数列的首项a1的取值范围是 .
| lim |
| n→∞ |
考点:数列的求和,数列的极限
专题:计算题,等差数列与等比数列
分析:依题意知|q|<1且q≠0,由
Sn=
=2⇒q=1-
∈(-1,1),从而可求得a1的取值范围.
| lim |
| n→∞ |
| a1 |
| 1-q |
| a1 |
| 2 |
解答:
解:依题意知|q|<1且q≠0,
∴Sn=
,
∴
Sn=
,
∵
Sn=2,
∴
=2,
∴q=1-
∈(-1,1),q≠0,
即-1<
-1<1且
-1≠0,
解得0<a1<2或2<a1<4.
故答案为:(0,2)∪(2,4).
∴Sn=
| a1(1-qn) |
| 1-q |
∴
| lim |
| n→∞ |
| a1 |
| 1-q |
∵
| lim |
| n→∞ |
∴
| a1 |
| 1-q |
∴q=1-
| a1 |
| 2 |
即-1<
| a1 |
| 2 |
| a1 |
| 2 |
解得0<a1<2或2<a1<4.
故答案为:(0,2)∪(2,4).
点评:本题考查数列的求和与数列的极限,求得q=1-
是关键,考查转化思想与运算能力,属于中档题.
| a1 |
| 2 |

练习册系列答案
相关题目
过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤9}分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
| A、x+y-2=0 |
| B、y-1=0 |
| C、x-y=0 |
| D、x+3y-4=0 |
某几何体的三视图(如图),则该几何体的体积是( )
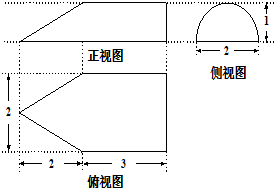

A、
| ||
B、
| ||
C、
| ||
D、
|
平行四边形ABCD中,E为CD的中点.若在平行四边形ABCD内部随机取一点M,则点M取自△ABE内部的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知△ABC和点M满足
+
+2
=
.若存在实数m使得
+
=m
成立,则m=( )
| MA |
| MB |
| MC |
| 0 |
| CA |
| CB |
| CM |
| A、2 | B、3 | C、4 | D、5 |
 已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.