题目内容
 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )| A、16π | ||
B、
| ||
| C、12π | ||
| D、36π |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图.
解答:
解:由三视图可知,
该几何体的体积为圆柱体积的
;
设圆柱的底面圆的半径为r,则r+
r=3;
解得r=2;
故圆柱的体积V=4π×4=16π;
故该几何体的体积为
π;
故选B.
该几何体的体积为圆柱体积的
| 1 |
| 3 |
设圆柱的底面圆的半径为r,则r+
| 1 |
| 2 |
解得r=2;
故圆柱的体积V=4π×4=16π;
故该几何体的体积为
| 16 |
| 3 |
故选B.
点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
相关题目
点(1,0,4)在空间直角坐标系中的位置是( )
| A、y轴上 |
| B、xOy平面上 |
| C、xOz平面上 |
| D、yOz平面上 |
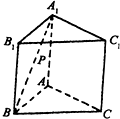 如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.