题目内容
已知三角形的三个顶点分别是A(-5,0),B(3,-3),C(0,2)
(1)求△ABC的面积,
(2)若直线l过点C且与A、B的距离相等,求直线l的方程.
(1)求△ABC的面积,
(2)若直线l过点C且与A、B的距离相等,求直线l的方程.
考点:三角形的面积公式,两条平行直线间的距离
专题:直线与圆
分析:(1)由两点间的距离公式可得|AB|,由点到直线的距离公式可得三角形的高h,由面积公式可得△ABC的面积;
(2)当直线l与AB平行或过AB中点(-1,-
)时满足题意,分别由条件求其方程可得.
(2)当直线l与AB平行或过AB中点(-1,-
| 3 |
| 2 |
解答:
解:(1)∵三角形的三个顶点分别是A(-5,0),B(3,-3),C(0,2),
∴|AB|=
=
,kAB=
=-
,
∴直线AB的方程为y=-
(x+5),即3x+8y+15=0,
由点到直线的距离公式可得三角形的高h=
=
∴△ABC的面积S=
×
×
=
,
(2)当直线l与AB平行时满足题意,可得方程为y-2=-
(x-0),即3x+8y-16=0;
当直线l过AB中点(-1,-
)时满足题意,可得斜率为
=
,
可得方程为y-2=
(x-0),即7x-2y+4=0,
∴直线l的方程为:3x+8y-16=0或7x-2y+4=0
∴|AB|=
| (-5-3)2+(0+3)2 |
| 73 |
| 0+3 |
| -5-3 |
| 3 |
| 8 |
∴直线AB的方程为y=-
| 3 |
| 8 |
由点到直线的距离公式可得三角形的高h=
| |0+16+15| | ||
|
| 31 | ||
|
∴△ABC的面积S=
| 1 |
| 2 |
| 73 |
| 31 | ||
|
| 31 |
| 2 |
(2)当直线l与AB平行时满足题意,可得方程为y-2=-
| 3 |
| 8 |
当直线l过AB中点(-1,-
| 3 |
| 2 |
-
| ||
| -1-0 |
| 7 |
| 2 |
可得方程为y-2=
| 7 |
| 2 |
∴直线l的方程为:3x+8y-16=0或7x-2y+4=0
点评:本题考查三角形的面积,涉及距离公式和平行关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )| A、16π | ||
B、
| ||
| C、12π | ||
| D、36π |
xOy平面内点的坐标的特点是( )
| A、z坐标是0 |
| B、x坐标和y坐标都是0 |
| C、x坐标是0 |
| D、x坐标,y坐标和z坐标不可能都是0 |
执行如图所示的程序框图,则输出的y=( )


| A、0.5 | B、1 | C、-1 | D、2 |
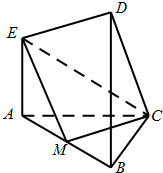 如图,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点
如图,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点