题目内容
设函数f(x)=
,若区间(0,4]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤1的概率为 .
|
考点:几何概型
专题:概率与统计
分析:由题意知本题是一个几何概型,概率的值为对应长度之比,根据题目中所给的不等式解出解集,解集在数轴上对应的线段的长度之比等于要求的概率.
解答:
解:由题意区间(0,4]内随机选取一个实数x0,所选取的实数x0满足的区域长度为4,
所选取的实数x0满足f(x0)≤1的范围是
和
的解集的并集,
解得{x|
≤x≤1}和{x|1<x≤2},
所以所选取的实数x0满足f(x0)≤1的x0的范围是[
,2],区域长度为
,
所以所选取的实数x0满足f(x0)≤1的概率为
=
;
故答案为:
所选取的实数x0满足f(x0)≤1的范围是
|
|
解得{x|
| 1 |
| 2 |
所以所选取的实数x0满足f(x0)≤1的x0的范围是[
| 1 |
| 2 |
| 3 |
| 2 |
所以所选取的实数x0满足f(x0)≤1的概率为
| ||
| 4 |
| 3 |
| 8 |
故答案为:
| 3 |
| 8 |
点评:本题主要考查了几何概型,以及分段函数对应的不等式的解法,关键是明确事件对应的区域长度.

练习册系列答案
相关题目
 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为120°的扇形,则该几何体的体积为( )| A、16π | ||
B、
| ||
| C、12π | ||
| D、36π |
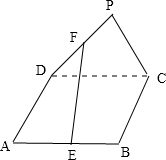 如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.
如图,点P为正方形ABCD所在平面外的一点,E、F分别是AB、PD的中点.求证:EF∥平面PBC.