题目内容
4.已知各项不为零的数列{an}的前n项的和为Sn,且满足Sn=λan-1,若{an}为递增数列,则λ的取值范围为λ<0或λ>1.分析 n=1时,a1=λa1-1,λ≠1,解得a1=$\frac{1}{λ-1}$.n≥2时,an=Sn-Sn-1,化为:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{λ}{λ-1}$.由于{an}为递增数列,对λ分类讨论即可得出.
解答 解:n=1时,a1=λa1-1,λ≠1,解得a1=$\frac{1}{λ-1}$.
n≥2时,an=Sn-Sn-1=λan-1-(λan-1-1),化为:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{λ}{λ-1}$.
∵{an}为递增数列,∴λ>1时,$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{λ}{λ-1}$>1,恒成立,因此λ>1.
λ<1时,$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{λ}{λ-1}$∈(0,1),解得λ<0.
故答案为:λ<0或λ>1.
点评 本题考查了数列递推关系、等比数列的定义通项公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
15.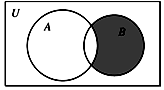 设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
 设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {2,4,6} |
19.斜率为k(k>0)的直线经过抛物线y2=2px(p>0)的焦点,与抛物线交于A、B两点,与抛物线的准线交于C点,当B为AC中点时,k的值为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
9.某公司某件产品的定价x与销量y之间的数据统计表如下,根据数据,用最小二乘法得出y与x的线性回归直线方程为:$\widehat{y}$=6.5$\widehat{x}$+17.5,则表格中n的值应为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | n | 50 | 70 |
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
16.已知数列{an}的前n项和为Sn,且对任意正整数n都有an=$\frac{3}{4}$Sn+2成立.若bn=log2an,则b1008=( )
| A. | 2017 | B. | 2016 | C. | 2015 | D. | 2014 |
14.数列{an}满足a1=$\frac{{\sqrt{2}}}{8}$,a2=$\frac{{\sqrt{33}}}{33}$,(an>0),$\frac{{{a}_{n}}^{2}-{{a}_{n-1}}^{2}}{{{a}_{n-1}}^{2}}$=$\frac{{{a}_{n+1}}^{2}-{{a}_{n}}^{2}}{{{a}_{n+1}}^{2}}$(n≥2),则a2017=( )
| A. | $\frac{{\sqrt{3}}}{64}$ | B. | $\frac{{\sqrt{2}}}{64}$ | C. | $\frac{1}{32}$ | D. | $\frac{33}{32}$ |