题目内容
12.渔场中鱼群的最大养殖量为m,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量,已知鱼群的年增长量y吨和实际养殖量x吨与空闲率的乘积成正比,比例系数为k(k>0),则鱼群年增长量的最大值是$\frac{km}{4}$.分析 由鱼群的年增长量y吨和实际养殖量x吨与空闲率的乘积成正比,比例系数为k(k>0).我们根据题意求出空闲率,即可得到y关于x的函数关系式,并指出这个函数的定义域,使用配方法,易分析出鱼群年增长量的最大值.
解答 解:由题意,空闲率为 1-$\frac{x}{m}$,
∴y=kx(1-$\frac{x}{m}$),定义域为(0,m),
y=kx(1-$\frac{x}{m}$)=-$\frac{k}{m}(x-\frac{m}{2})^{2}+\frac{km}{4}$,
因为 x∈(0,m),k>0;
所以当x=$\frac{m}{2}$时,ymax=$\frac{km}{4}$.
故答案为$\frac{km}{4}$.
点评 函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
17.圆C与x轴相切于T(1,0),与y轴正半轴交于两点A、B,且|AB|=2,则圆C的标准方程为( )
| A. | (x-1)2+(y-$\sqrt{2}$)2=2 | B. | (x-1)2+(y-2)2=2 | C. | (x+1)2+(y+$\sqrt{2}$)2=4 | D. | (x-1)2+(y-$\sqrt{2}$)2=4 |
3.某几何体的三视图如图所示,则该几何体的体积是( )
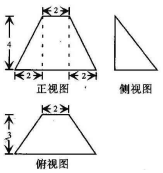

| A. | 16 | B. | 20 | C. | 52 | D. | 60 |