设全集U=N*.集合A={1.2.3.5}.B={2.4.6}.则图中的阴影部分表示的集合为( )A．{2}B．{4.6}C．{1.3.5}D．{2.4.6} 题目和参考答案——青夏教育精英家教网——

题目内容

15．

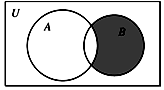设全集U=N*，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（　　）

A．

{2}

B．

{4，6}

C．

{1，3，5}

D．

{2，4，6}

分析由韦恩图可知阴影部分表示的集合为（C_UA）∩B，根据集合的运算求解即可．

解答解：由韦恩图可知阴影部分表示的集合为（C_UA）∩B，
∴（C_UA）∩B={4，6}．
故选B

点评本小题主要考查Venn图表达集合的关系及运算、Venn图的应用等基础知识，考查数形结合思想．属于基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

5．已知过抛物线G：y²=2px（p＞0）焦点F的直线l与抛物线G交于M、N两点（M在x轴上方），满足$\overrightarrow{MF}=3\overrightarrow{FN}$，$|{MN}|=\frac{16}{3}$，则以M为圆心且与抛物线准线相切的圆的标准方程为（　　）

	A．	${（{x-\frac{1}{3}}）^2}+{（{y-\frac{{2\sqrt{3}}}{3}}）^2}=\frac{16}{3}$		B．	${（{x-\frac{1}{3}}）^2}+{（{y-\frac{{\sqrt{3}}}{3}}）^2}=\frac{16}{3}$
	C．	${（{x-3}）^2}+{（{y-2\sqrt{3}}）^2}=16$		D．	${（{x-3}）^2}+{（{y-\sqrt{3}}）^2}=16$

6．过点M（2，-2p）引抛物线x²=2py（p＞0）的切线，切点分别为A，B，若$|{AB}|=4\sqrt{10}$，则p的值是（　　）

3．若圆锥曲线Γ：$\frac{x^2}{m}+\frac{y^2}{5}$=1（m≠0且m≠5）的一个焦点与抛物线y²=8x的焦点重合，则实数m=（　　）

10．已知M是抛物线C：y²=2px（p＞0）上一点，F是抛物线C的焦点，若|MF|=p，K是抛物线C的准线与x轴的交点，则∠MKF=（　　）

20．一袋中有7个大小相同的小球，其中有2个红球，3个黄球，2个蓝球，从中任取3个小球．
（I）求红、黄、蓝三种颜色的小球各取1个的概率；
（II）设X表示取到的蓝色小球的个数，求X的分布列和数学期望．

7．若正项等比数列{a_n}，已知a₁=4且a₅²=16a₂•a₆，则$\frac{1}{\sqrt{{a}_{1}}}$+$\frac{2}{\sqrt{{a}_{2}}}$+$\frac{3}{\sqrt{{a}_{3}}}$+…+$\frac{n}{\sqrt{{a}_{n}}}$=2-$\frac{n+2}{{2}^{n}}$．

4．已知各项不为零的数列{a_n}的前n项的和为S_n，且满足S_n=λa_n-1，若{a_n}为递增数列，则λ的取值范围为λ＜0或λ＞1．

祖冲之之子祖暅是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等．此即祖暅原理．利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为h（0＜h＜2）的平面截该几何体，则截面面积为（　　）