题目内容
19.斜率为k(k>0)的直线经过抛物线y2=2px(p>0)的焦点,与抛物线交于A、B两点,与抛物线的准线交于C点,当B为AC中点时,k的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
分析 如图,设A,B两点的抛物线的准线上的射影分别为E,M,过B作AE的垂线BN,在三角形ABN中,∠BAN等于直线AB的倾斜角,其正切值即为k值,利用在直角三角形ABN中,tan∠BAN=$\frac{BN}{AN}$,从而得出直线AB的斜率.
解答 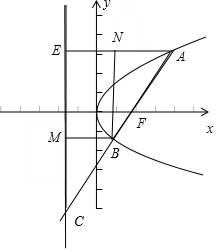 解:如图,设A,B两点的抛物线的准线上的射影分别为E,M,
解:如图,设A,B两点的抛物线的准线上的射影分别为E,M,
过B作AE的垂线BN,
在三角形ABN中,∠BAN等于直线AB的倾斜角,其正切值即为k值,
设|BF|=n,B为AC中点,可得2|BF|=|AE|,即|AF|=2|BF|,∴|AF|=2n,
根据抛物线的定义得:|AE|=2n,|BF|=n,
∴|AN|=n,
在直角三角形ABC中,tan∠BAN=$\frac{BN}{AN}$=$\frac{\sqrt{9{n}^{2}-{n}^{2}}}{n}$=2$\sqrt{2}$;
故选:C.
点评 本题主要考察了直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要善于运用抛物线的定义解决问题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
10.已知M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,若|MF|=p,K是抛物线C的准线与x轴的交点,则∠MKF=( )
| A. | 45° | B. | 30° | C. | 15° | D. | 60° |
11.设命题p:若y=f(x)的定义域为R,且函数y=f(x-2)图象关于点(2,0)对称,则函数y=f(x)是奇函数,命题q:?x≥0,x${\;}^{\frac{1}{2}}$≥x${\;}^{\frac{1}{3}}$,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | ¬p∧¬q |
10.已知正三棱锥P-ABC的外接球的球心O满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=0,则二面角A-PB-C的正弦值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{\sqrt{6}}{3}$ |
 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.