题目内容
在等比数列{an}中,若a1+a2+a3=
,a2=
,
+
+
= .
| 5 |
| 3 |
| 1 |
| 3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
考点:数列的求和
专题:等差数列与等比数列
分析:由a1+a2+a3=
,a2 =
,利用等比数列的性质能推导出a1+a3=
,a1a3=a22=
,由此能求出
+
+
.
| 5 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 9 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
解答:
解:在等比数列{an}中,
∵a1+a2+a3=
,a2 =
,
∴a1+a3=
,a1a3=a22=
,
∴
+
+
=(
+
)+
=
+3=
+3=15.
故答案为:15.
∵a1+a2+a3=
| 5 |
| 3 |
| 1 |
| 3 |
∴a1+a3=
| 4 |
| 3 |
| 1 |
| 9 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a3 |
| 1 |
| a2 |
=
| a1+a3 |
| a1a3 |
| ||
|
故答案为:15.
点评:本题考查等比数列的性质及其应用,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
函数f(x)=sin(x+φ)+cos(x+φ)为奇函数,则φ的一个可能取值( )
| A、0 | ||
B、
| ||
C、-
| ||
D、-
|
若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)+f(x-1)的定义域为( )
| A、[-1,0] |
| B、[-1,1] |
| C、[0,1] |
| D、[-5,-2] |
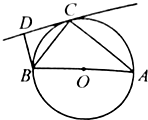 如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=
如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=