题目内容
设x，y∈R，命题p：|x-y|＜1，命题q：|x|＜|y|+1，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：由绝对值不等式的性质可得：|x|-|y|≤|x-y|＜1⇒|x|＜|y|+1，反之不成立，即可判断出．
解答：
解：由绝对值不等式的性质可得：|x|-|y|≤|x-y|＜1⇒|x|＜|y|+1，反之不成立，例如|-2|＜|3|+1，但是|-2-3|＜1不成立．
因此p是q的充分不必要条件．
故选：A．
因此p是q的充分不必要条件．
故选：A．
点评：本题考查了绝对值不等式的性质、简易逻辑的判定方法，考查了推理能力，属于基础题．
练习册系列答案
相关题目
根据表格中的数据，可以判定方程ex-x-6=0的一个根所在的区间为（ ）
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
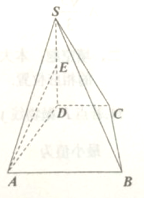如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD垂直于AB和CD，侧棱SD⊥底面ABCD，且SD=AD=AB=2CD，点E为棱SD的中点．求异面直线AE和SB所成角的余弦值．已知命题p：当0＜x＜2时x2＜4，命题q：当b＜a＜0时b2＜a2，则（ ）
| A、p∧（￢q）为真 |
| B、p∧q为真 |
| C、（￢p）∨q为真 |
| D、（￢p）∧q为真 |