题目内容
为了得到函数y=2sin(2x+
)的图象,只需把函数y=2sinx的图象( )
| π |
| 6 |
A、向左平移
| ||||
B、向左平移
| ||||
C、各点的纵坐标不变、横坐标变为原来的2倍,再把所得图象向左平移
| ||||
D、各点的纵坐标不变、横坐标变为原来的
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:把函数y=2sinx的图象向左平移
个单位长度,得到的函数解析式为:y=2sin(x+
),
再把所得各点的横坐标变为原来的
倍(纵坐标不变),得到的函数解析式为:y=2sin(2x+
),
故选:B.
| π |
| 6 |
| π |
| 6 |
再把所得各点的横坐标变为原来的
| 1 |
| 2 |
| π |
| 6 |
故选:B.
点评:本题考查的知识要点:函数图象的变换问题平移变换和伸缩变换,属于基础题型.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
设变量x、y满足约束条件
,则z=2x-2y的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若某算法框图如图所示,则输出的结果为( )
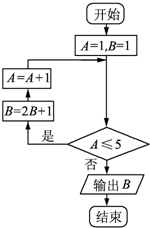

| A、7 | B、15 | C、31 | D、63 |
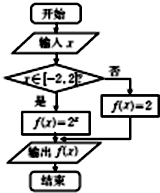 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2,-1] |
| B、(-∞,-1] |
| C、[-1,2] |
| D、[2,+∞) |
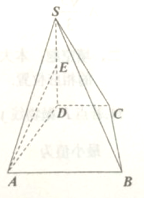 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.