题目内容
用20米长的篱笆一边靠墙围成矩形,问靠墙一边的长度为何值时,场地的面积最大,最大面积是多少?
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:由题意可得:x+2y=l,x>0,y>0.利用基本不等式即可得出xy的最大值.
解答:
解:设靠墙一边为xm,相邻边ym,x+2y=20,面积S=xy,
20=x+2y≥2
,∴xy≤50,当x=10,S最大值50.
∴靠墙一边的长度为10米时,场地的面积最大,最大面积是50cm2.
20=x+2y≥2
| 2xy |
∴靠墙一边的长度为10米时,场地的面积最大,最大面积是50cm2.
点评:本题考查了基本不等式的性质和矩形的面积,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=1+2
sinxcosx-2
sin2x,x∈R.
(1)求函数f(x)的单调增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=3,b=
,f(A)=1,求角C.
| 3 |
| 3 |
(1)求函数f(x)的单调增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=3,b=
| 3 |
已知点P在圆C:x2+y2=2x+2y上,则点P到直线l:x+y+1=0的距离最大值为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、3
|
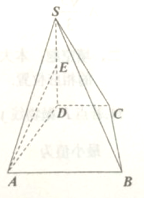 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.