题目内容
3.已知$\overrightarrow a$=(2sinα,1),$\overrightarrow b$=(cosα,1),α∈(0,$\frac{π}{4}$).(1)若$\overrightarrow a$∥$\overrightarrow b$,求tanα的值;
(2)若$\overrightarrow a$•$\overrightarrow b$=$\frac{9}{5}$,求sin(2α+$\frac{π}{4}$)的值.
分析 (1)由$\overrightarrow{a}∥\overrightarrow{b}$即可得到2sinα-cosα=0,从而可求出tanα的值;
(2)进行数量积的坐标运算,根据$\overrightarrow{a}•\overrightarrow{b}=\frac{9}{5}$即可求得$sin2α=\frac{4}{5}$,由α的范围便可求出cos2α的值,从而求出$sin(2α+\frac{π}{4})$的值.
解答 解:(1)∵$\overrightarrow{a}∥\overrightarrow{b}$;
∴2sinα-cosα=0;
∴2sinα=cosα;
∴$tanα=\frac{1}{2}$;
(2)$\overrightarrow{a}•\overrightarrow{b}=2sinαcosα+1=sin2α+1=\frac{9}{5}$;
∴$sin2α=\frac{4}{5}$;
∵$α∈(0,\frac{π}{4})$;
∴$2α∈(0,\frac{π}{2})$;
∴$cos2α=\frac{3}{5}$;
∴$sin(2α+\frac{π}{4})=sin2αcos\frac{π}{4}+cos2αsin\frac{π}{4}$=$\frac{4}{5}×\frac{\sqrt{2}}{2}+\frac{3}{5}×\frac{\sqrt{2}}{2}=\frac{7\sqrt{2}}{10}$.
点评 考查向量平行的坐标关系,数量积的坐标运算,以及两角和的正弦公式.

练习册系列答案
相关题目
11.设a=lg$\frac{2}{3}$,b=lg$\frac{2}{5}$,c=lg$\frac{3}{2}$,则( )
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |
3.已知集合A={x|(x-1)(3-x)<0},B={x|-2≤x≤2},则A∩B=( )
| A. | [-2,1) | B. | (1,2] | C. | [-2,-1) | D. | (-1,2] |
7.下列运算中,正确的是( )
| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
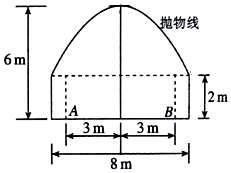 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?