题目内容
 某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(1)求出第4组的频率;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据频率分步直方图的性质,根据所给的频率分步直方图中小矩形的长和宽,求出矩形的面积,即这组数据的频率.
(2)根据概率公式计算,事件“5位同学中抽两位同学”有10种可能,而且这些事件的可能性相同,其中事件“至少有一人是“优秀””可能种数是9,那么即可求得事件M的概率.
(2)根据概率公式计算,事件“5位同学中抽两位同学”有10种可能,而且这些事件的可能性相同,其中事件“至少有一人是“优秀””可能种数是9,那么即可求得事件M的概率.
解答:
 解:(1)其它组的频率为
解:(1)其它组的频率为
(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,…(5分)
(2)依题意良好的人数为40×0.4=16人,优秀的人数为40×0.6=24人
优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,记从这5人中选2人至少有1人是优秀为事件M,将考试成绩优秀的三名学生记为A,B,C,考试成绩良好的两名学生记为a,b 从这5人中任选2人的所有基本事件包括:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab共10个基本事件
事件M含的情况是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9个
所以P(M)=
…(12分)
 解:(1)其它组的频率为
解:(1)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,…(5分)
(2)依题意良好的人数为40×0.4=16人,优秀的人数为40×0.6=24人
优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,记从这5人中选2人至少有1人是优秀为事件M,将考试成绩优秀的三名学生记为A,B,C,考试成绩良好的两名学生记为a,b 从这5人中任选2人的所有基本事件包括:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab共10个基本事件
事件M含的情况是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9个
所以P(M)=
| 9 |
| 10 |
点评:本题考查频率分步直方图的性质,考查等可能事件的概率,本题是一个概率与统计的综合题目.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
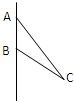 如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是
如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是