题目内容
已知函数f(x)=lnx+a(x2-x)
(1)若a=-1,求证f(x)有且仅有一个零点;
(2)若对于x∈[1,2],函数f(x)图象上任意一点处的切线的倾斜角都不大于
,求实数a的取值范围;
(3)若f(x)存在单调递减区间,求实数a的取值范围.
(1)若a=-1,求证f(x)有且仅有一个零点;
(2)若对于x∈[1,2],函数f(x)图象上任意一点处的切线的倾斜角都不大于
| π |
| 4 |
(3)若f(x)存在单调递减区间,求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程,函数的零点,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导函数,求得函数的单调性,求出函数的最值,即可得证结论;
(2)由已知,0≤f'(x)≤1在x∈[1,2]上恒成立,分离参数求最值,可求实数a的取值范围;
(3)f(x)存在单调递减区间,等价于f′(x)=
<0在(0,+∞)上有解,即2ax2-ax+1<0在(0,+∞)上有解,分类讨论求最值,即可求实数a的取值范围.
(2)由已知,0≤f'(x)≤1在x∈[1,2]上恒成立,分离参数求最值,可求实数a的取值范围;
(3)f(x)存在单调递减区间,等价于f′(x)=
| 2ax2-ax+1 |
| x |
解答:
(1)证明:f(x)=lnx-x2+x(x>0),f′(x)=
-2x+1=
令f'(x)=0,得x=1,
令f'(x)>0,∵x>0,∴0<x<1;令f'(x)<0,
∵x>0,∴x>1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
∴f(x)最大值=f(1)=0,
∴f(x)有且仅有一个零点,该零点即为1.---------(4分)
(2)解:f′(x)=
,由已知,0≤f'(x)≤1在x∈[1,2]上恒成立.---------(6分)
由f'(x)≤1在x∈[1,2]上恒成立,可得a≤(
)min=0
由f'(x)≥0在x∈[1,2]上恒成立,可得a≥(
)max=-
∴-
≤a≤0-------------------(10分)
(3)解:f(x)存在单调递减区间,等价于f′(x)=
<0在(0,+∞)上有解,即2ax2-ax+1<0在(0,+∞)上有解
记g(x)=2ax2-ax+1,x∈(0,+∞)
当a=0时,g(x)=1,不满足条件;
当a<0时,g(x)为开口向下的二次函数,2ax2-ax+1<0在(0,+∞)上恒有解;
当a>0时,g(x)为开口向上的二次函数,对称轴为x=
,2ax2-ax+1<0在(0,+∞)上有解,只需g(x)min>0,即g(
)>0,解得a>8
综上所述,a的取值范围为(-∞,0)∪(8,+∞)
| 1 |
| x |
| -(x-1)(2x+1) |
| x |
令f'(x)=0,得x=1,
令f'(x)>0,∵x>0,∴0<x<1;令f'(x)<0,
∵x>0,∴x>1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
∴f(x)最大值=f(1)=0,
∴f(x)有且仅有一个零点,该零点即为1.---------(4分)
(2)解:f′(x)=
| 2ax2-ax+1 |
| x |
由f'(x)≤1在x∈[1,2]上恒成立,可得a≤(
| x-1 |
| 2x2-x |
由f'(x)≥0在x∈[1,2]上恒成立,可得a≥(
| -1 |
| 2x2-x |
| 1 |
| 6 |
∴-
| 1 |
| 6 |
(3)解:f(x)存在单调递减区间,等价于f′(x)=
| 2ax2-ax+1 |
| x |
记g(x)=2ax2-ax+1,x∈(0,+∞)
当a=0时,g(x)=1,不满足条件;
当a<0时,g(x)为开口向下的二次函数,2ax2-ax+1<0在(0,+∞)上恒有解;
当a>0时,g(x)为开口向上的二次函数,对称轴为x=
| 1 |
| 4 |
| 1 |
| 4 |
综上所述,a的取值范围为(-∞,0)∪(8,+∞)
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生分析转化问题的能力,属于中档题.

练习册系列答案
相关题目
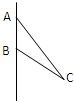 如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是
如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是