题目内容
动圆C与定圆C1:(x+3)2+y2=9,C2:(x-3)2+y2=1都外切,求动圆圆心C的轨迹方程.
考点:轨迹方程
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:由动圆与两定圆外切得到圆心距与半径之间的关系,作差后得到动圆圆心C的轨迹符合双曲线定义,由已知求出实半轴和虚半轴,则动圆圆心C的轨迹方程可求.
解答:
解:设所求圆的圆心坐标C(x,y),半径为r,
两定圆的圆心分别是C1,C2,半径分别为3,1.
∵所求圆与两个圆都外切,
∴|CC1|=r+3,|CC2|=r+1,
即|CC1|-|CC2|=2,
根据双曲线定义可知C点的轨迹为以C1,C2为焦点的双曲线的右支,
由2c=6,c=3;2a=2,a=1,∴b=
=2
.
∴C点的轨迹方程为x2-
=1(x≥1).
两定圆的圆心分别是C1,C2,半径分别为3,1.
∵所求圆与两个圆都外切,
∴|CC1|=r+3,|CC2|=r+1,
即|CC1|-|CC2|=2,
根据双曲线定义可知C点的轨迹为以C1,C2为焦点的双曲线的右支,
由2c=6,c=3;2a=2,a=1,∴b=
| 9-1 |
| 2 |
∴C点的轨迹方程为x2-
| y2 |
| 8 |
点评:本题考查了轨迹方程的求法,考查了圆与圆的位置关系,训练了利用定义求双曲线的方程,是中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
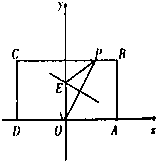 如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足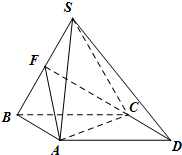 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
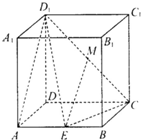 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.