题目内容
探究函数f(x)=x+
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
(1)写出f(x)=x+
,x∈(0,+∞)的单调区间;
(2)证明:函数f(x)=x+
(x>0)在区间(0,2)单调递减;
(3)若不等式2x-2k≤1-
对x<0恒成立,求实数k的取值范围.
| 4 |
| x |
| x | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 |
| y | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 |
(1)写出f(x)=x+
| 4 |
| x |
(2)证明:函数f(x)=x+
| 4 |
| x |
(3)若不等式2x-2k≤1-
| 8 |
| x |
考点:函数恒成立问题
专题:不等式的解法及应用
分析:(1)根据表格数据,即可写出f(x)=x+
,x∈(0,+∞)的单调区间;
(2)根据函数单调性的定义即可证明:函数f(x)=x+
(x>0)在区间(0,2)单调递减;
(3)将不等式2x-2k≤1-
对x<0恒成立转化为最值恒成立,即可求实数k的取值范围.
| 4 |
| x |
(2)根据函数单调性的定义即可证明:函数f(x)=x+
| 4 |
| x |
(3)将不等式2x-2k≤1-
| 8 |
| x |
解答:
解:(1)由表格数据可知当0<x<2时,函数单调递减,当x>2时函数单调递增,
即f(x)=x+
,x∈(0,+∞)的单调递增区间为[2,+∞),递减区间为(0,2];
(2)证明:函数f(x)=x+
(x>0)在区间(0,2)单调递减;
设0<x1<x2<2,
则f(x1)-f(x2)=x1+
-x2-
=(x1-x2)+
=(x1-x2)(1-
)=(x1-x2)?
,
∵0<x1<x2<2,
∴x1-x2<0,x1x2-4<0,
∴f(x1)-f(x2)=(x1-x2)?
>0,
即f(x1)-f(x2)>0,
∴f(x1)>f(x2),
即函数f(x)=x+
(x>0)在区间(0,2)单调递减.
(3)若不等式2x-2k≤1-
对x<0恒成立,
则等价为2x+
≤1+2k,
即x+
≤
,
设g(x)=x+
,
则g(x)在{x|x≠0}上为奇函数,
∴根据奇函数的对称性可知,函数在(-∞,-2)上单调递增,在(-2,0)上单调递减,
∴当x<0时,函数的最大值为g(-2)=-2-2=-4,
∴要使x+
≤
恒成立,
则
≥-4,
解得k≥-
,
实数k的取值范围是k≥-
.
即f(x)=x+
| 4 |
| x |
(2)证明:函数f(x)=x+
| 4 |
| x |
设0<x1<x2<2,
则f(x1)-f(x2)=x1+
| 4 |
| x1 |
| 4 |
| x2 |
| 4(x2-x1) |
| x1x2 |
| 4 |
| x1x2 |
| x1x2-4 |
| x1x2 |
∵0<x1<x2<2,
∴x1-x2<0,x1x2-4<0,
∴f(x1)-f(x2)=(x1-x2)?
| x1x2-4 |
| x1x2 |
即f(x1)-f(x2)>0,
∴f(x1)>f(x2),
即函数f(x)=x+
| 4 |
| x |
(3)若不等式2x-2k≤1-
| 8 |
| x |
则等价为2x+
| 8 |
| x |
即x+
| 4 |
| x |
| 1+2k |
| 2 |
设g(x)=x+
| 4 |
| x |
则g(x)在{x|x≠0}上为奇函数,
∴根据奇函数的对称性可知,函数在(-∞,-2)上单调递增,在(-2,0)上单调递减,
∴当x<0时,函数的最大值为g(-2)=-2-2=-4,
∴要使x+
| 4 |
| x |
| 1+2k |
| 2 |
则
| 1+2k |
| 2 |
解得k≥-
| 9 |
| 2 |
实数k的取值范围是k≥-
| 9 |
| 2 |
点评:本题主要考查基本不等式的应用,要求熟练掌握基本不等式的应用,将不等式恒成立转化为求函数的最值是解决本题的关键.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,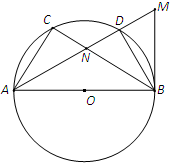 如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.
如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM. 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=